浙江省温州市平阳县2019届数学中考一模试卷
试卷更新日期:2019-09-03 类型:中考模拟
一、单选题
-
1. ﹣2的绝对值是( )A、2 B、﹣2 C、 D、-2. 如图所示的几何体是由一个长方体和一个圆柱体组成,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 根据PM2.5空气质量标准:24小时PM2.5均值在1~35(微克/立方米)的空气质量等级为优.将环保部门对我市PM2.5一周的检测数据制作成如下统计表.这组PM2.5数据的中位数是( )
3. 根据PM2.5空气质量标准:24小时PM2.5均值在1~35(微克/立方米)的空气质量等级为优.将环保部门对我市PM2.5一周的检测数据制作成如下统计表.这组PM2.5数据的中位数是( )天数
2
1
1
2
1
PM2.5
18
20
21
29
30
A、18微克/立方米 B、20微克/立方米 C、21微克/立方米 D、25微克/立方米4. 已知a为整数,且 ,则a等于( )A、1 B、2 C、3 D、45. 若关于x的一元二次方程x2﹣2x﹣k+1=0有两个相等的实数根,则k的值是( )A、﹣1 B、0 C、1 D、26. 如图,在平面直角坐标系中,△ABC位于第一象限,点A的坐标是(4,3),把△ABC向左平移6个单位长度,得到△A1B1C1 , 则点B1的坐标是( ) A、(﹣2,3) B、(3,﹣1) C、(﹣3,1) D、(﹣5,2)7. 化简 的结果是( )A、a+1 B、a﹣1 C、a2﹣a D、a8. 某旅店一共70个房间,大房间每间住8个人,小房间每间住6个人,一共480个学生刚好住满,设大房间有 个,小房间有 个.下列方程正确的是( )A、 B、 C、 D、9. 如图,△ABC是等边三角形,AB=4,D为AB的中点,点E,F分别在线段AD,BC上,且BF=2AE,连结EF交中线AD于点G,连结BG,设AE=x(0<x<2),△BEG的面积为y,则y关于x的函数表达式是( )
A、(﹣2,3) B、(3,﹣1) C、(﹣3,1) D、(﹣5,2)7. 化简 的结果是( )A、a+1 B、a﹣1 C、a2﹣a D、a8. 某旅店一共70个房间,大房间每间住8个人,小房间每间住6个人,一共480个学生刚好住满,设大房间有 个,小房间有 个.下列方程正确的是( )A、 B、 C、 D、9. 如图,△ABC是等边三角形,AB=4,D为AB的中点,点E,F分别在线段AD,BC上,且BF=2AE,连结EF交中线AD于点G,连结BG,设AE=x(0<x<2),△BEG的面积为y,则y关于x的函数表达式是( ) A、 x2+ B、 + C、 + D、 +10. 勾股定理有着悠久的历史,它曾引起很多人的兴趣.英国佩里加(H.Perigal,1801﹣1898)用“水车翼轮法”(图1)证明了勾股定理.该证法是用线段QX,ST,将正方形BIJC分割成四个全等的四边形,再将这四个四边形和正方形ACYZ拼成大正方形AEFB(图2).若AD= ,tan∠AON= ,则正方形MNUV的周长为( )
A、 x2+ B、 + C、 + D、 +10. 勾股定理有着悠久的历史,它曾引起很多人的兴趣.英国佩里加(H.Perigal,1801﹣1898)用“水车翼轮法”(图1)证明了勾股定理.该证法是用线段QX,ST,将正方形BIJC分割成四个全等的四边形,再将这四个四边形和正方形ACYZ拼成大正方形AEFB(图2).若AD= ,tan∠AON= ,则正方形MNUV的周长为( )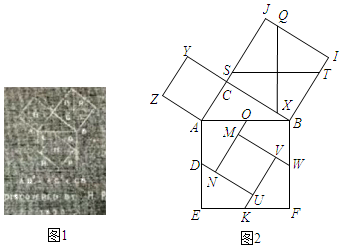 A、 B、18 C、16 D、
A、 B、18 C、16 D、二、填空题
-
11. 分解因式:x2﹣9= .
12. 已知一组数据6,x,3,3,5,2的众数是3和5,则这组数据的平均数是.13. 已知扇形的圆心角为120°,半径为6,则扇形的弧长是14. 为了改善生态环境,防止水土流失,红旗村计划在荒坡上种树960棵,由于青年志愿者支援,实际每天种树的棵数是原计划的2倍,结果提前4天完成任务,则原计划每天种树的棵数是.15. 如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B的坐标为( ,5),△ACD与△ACO关于直线AC对称(点D和O对应),反比例函数y= (k≠0)的图象与AB,BC分别交于E,F两点,连结DE,若DE∥x轴,则点F的坐标为. 16. 婷婷在发现一个门环的示意图如图所示.图中以正六边形ABCDEF的对角线AC的中点O为圆心,OB为半径作⊙O,AQ切⊙O于点P,并交DE于点Q,若AQ=12 cm,则该圆的半径为cm.
16. 婷婷在发现一个门环的示意图如图所示.图中以正六边形ABCDEF的对角线AC的中点O为圆心,OB为半径作⊙O,AQ切⊙O于点P,并交DE于点Q,若AQ=12 cm,则该圆的半径为cm.
三、解答题
-
17.(1)、计算: +(﹣1)2﹣20190(2)、化简:(a+2)2﹣a(a﹣3)18. 如图,在四边形ABCD中,AD∥BC,O是CD的中点,延长AO交BC的延长线于点E,且BC=CE.
 (1)、求证:△AOD≌△EOC;(2)、若∠BAE=90°,AB=6,OE=4,求AD的长.19. 艺术节期间,学校向学生征集书画作品,张老师从全校36个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作品的数量进行了分析统计,制作了两幅不完整的统计图.请根据相关信息,回答下列问题:
(1)、求证:△AOD≌△EOC;(2)、若∠BAE=90°,AB=6,OE=4,求AD的长.19. 艺术节期间,学校向学生征集书画作品,张老师从全校36个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作品的数量进行了分析统计,制作了两幅不完整的统计图.请根据相关信息,回答下列问题: (1)、请你将条形统计图补充完整,并估计全校共征集了多少件作品?(2)、如果全校征集的作品中有4件获得一等奖,其中有1名作者是男生,3名作者是女生,现要在获得一等奖的作者中选取两人参加表彰座谈会,求选取的两名学生恰好是一男一女的概率.(要求列表或画树状图)20. 如图,在12×8的方格纸中,ABCD的四个顶点都在格点上.
(1)、请你将条形统计图补充完整,并估计全校共征集了多少件作品?(2)、如果全校征集的作品中有4件获得一等奖,其中有1名作者是男生,3名作者是女生,现要在获得一等奖的作者中选取两人参加表彰座谈会,求选取的两名学生恰好是一男一女的概率.(要求列表或画树状图)20. 如图,在12×8的方格纸中,ABCD的四个顶点都在格点上. (1)、在图中,画出线段AE,使AE平分∠BAD,其中E是格点;(2)、在图中,画出线段CF,使CF⊥AB,其中F是格点.
(1)、在图中,画出线段AE,使AE平分∠BAD,其中E是格点;(2)、在图中,画出线段CF,使CF⊥AB,其中F是格点.
21. 如图,抛物线y=ax2+bx+5(a≠0)交直线y=kx+n(k>0)于A(1,1),B两点,交y轴于点C,直线AB交y轴于点D.已知该抛物线的对称轴为直线x= . (1)、求a,b的值;(2)、记直线AB与抛物线的对称轴的交点为E,连接CE,CB.若△CEB的面积为 ,求k,n的值.22. 如图,AB是⊙O的直径,D,E为⊙O上位于AB异侧的两点,连结BD并延长至点C,使得CD=BD,连结AC交⊙O于点F,连接BE,DE,DF.
(1)、求a,b的值;(2)、记直线AB与抛物线的对称轴的交点为E,连接CE,CB.若△CEB的面积为 ,求k,n的值.22. 如图,AB是⊙O的直径,D,E为⊙O上位于AB异侧的两点,连结BD并延长至点C,使得CD=BD,连结AC交⊙O于点F,连接BE,DE,DF. (1)、若∠E=35°,求∠BDF的度数.(2)、若DF=4,cos∠CFD= ,E是 的中点,求DE的长.23. 雾霾是对大气中各种悬浮颗粒物含量超标的笼统表述,雾霾的主要危害可归纳为两种:一是对人体产生危害,二是对交通产生危害.雾霾天气是一种大气污染状态,成都市区冬天雾霾天气比较严重,很多家庭兴起了为家里添置“空气清洁器”的热潮,为此,我市某商场根据民众健康要,代理销售某种进价为600元/台的家用“空气清洁器”.经过市场销售后发现:在一个月内,当售价是700元/台时,可售出350台,且售价每提高10元,就会少售出5台.(1)、试确定月销售量y(台)与售价x(元/台)之间的函数关系式;(2)、请计算当售价x(元台)定为多少时,该商场每月销售这种“空气清洁器”所获得的利润W(元)最大?最大利润是多少?(3)、若政府计划遴选部分商场,将销售“空气清洁器”纳入民生工程项目,规定:每销售一台“空气淸洁器”,财政补贴商家200元,但销售利润不能高于进价的25%,请问:该商场想获取最大利润,是否参与竞标此民生工程项目?并说明理由.24. 如图,矩形ABCD中,BC=8,点F是AB边上一点(不与点B重合)△BCF的外接圆交对角线BD于点E,连结CF交BD于点G.
(1)、若∠E=35°,求∠BDF的度数.(2)、若DF=4,cos∠CFD= ,E是 的中点,求DE的长.23. 雾霾是对大气中各种悬浮颗粒物含量超标的笼统表述,雾霾的主要危害可归纳为两种:一是对人体产生危害,二是对交通产生危害.雾霾天气是一种大气污染状态,成都市区冬天雾霾天气比较严重,很多家庭兴起了为家里添置“空气清洁器”的热潮,为此,我市某商场根据民众健康要,代理销售某种进价为600元/台的家用“空气清洁器”.经过市场销售后发现:在一个月内,当售价是700元/台时,可售出350台,且售价每提高10元,就会少售出5台.(1)、试确定月销售量y(台)与售价x(元/台)之间的函数关系式;(2)、请计算当售价x(元台)定为多少时,该商场每月销售这种“空气清洁器”所获得的利润W(元)最大?最大利润是多少?(3)、若政府计划遴选部分商场,将销售“空气清洁器”纳入民生工程项目,规定:每销售一台“空气淸洁器”,财政补贴商家200元,但销售利润不能高于进价的25%,请问:该商场想获取最大利润,是否参与竞标此民生工程项目?并说明理由.24. 如图,矩形ABCD中,BC=8,点F是AB边上一点(不与点B重合)△BCF的外接圆交对角线BD于点E,连结CF交BD于点G.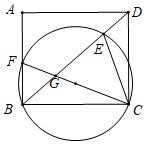 (1)、求证:∠ECG=∠BDC.(2)、当AB=6时,在点F的整个运动过程中.
(1)、求证:∠ECG=∠BDC.(2)、当AB=6时,在点F的整个运动过程中.①若BF=2 时,求CE的长.
②当△CEG为等腰三角形时,求所有满足条件的BE的长.
(3)、过点E作△BCF外接圆的切线交AD于点P.若PE∥CF且CF=6PE,记△DEP的面积为S1 , △CDE的面积为S2 , 请直接写出 的值.