浙江省温州市鹿城区2019届数学中考模拟试卷(3月)
试卷更新日期:2019-09-03 类型:中考模拟
一、单选题
-
1. 在0.3,﹣3,0,﹣ 这四个数中,最大的是( )A、0.3 B、﹣3 C、0 D、﹣2. 在开展“爱心捐助某灾区”的活动中,某团支部8名团员捐款的数额(单位:元)分别为3,5,6,5,5,6,5,10,这组数据的中位数是( )A、3元 B、5元 C、6元 D、10元3. 一个几何体的三视图如图所示,这个几何体是( )
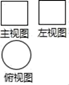 A、球 B、圆柱 C、圆锥 D、立方体4. 下列计算正确的是( )A、a2+a2=a4 B、2a2×a3=2 C、(a2)3=a6 D、3a﹣2a=15. 如图,在△ABC中,∠C=90°,AB=10,BC=6,则sin∠A=( )
A、球 B、圆柱 C、圆锥 D、立方体4. 下列计算正确的是( )A、a2+a2=a4 B、2a2×a3=2 C、(a2)3=a6 D、3a﹣2a=15. 如图,在△ABC中,∠C=90°,AB=10,BC=6,则sin∠A=( ) A、 B、 C、 D、6. 下列选项中,可以用来证明命题“若a2>b2 , 则a>b“是假命题的反例是( )A、a=﹣2,b=1 B、a=3,b=﹣2 C、a=0,b=1 D、a=2,b=17. 甲,乙工程队分别承接600米,800米的道路修建工程,已知乙比甲每天多修建12米,结果甲比乙提早1天完成,问甲每天修建多少米?设甲每天修建x米,根据题意可列出方程是( )A、 = ﹣1 B、 = +1 C、 = ﹣1 D、 = +18. 对于代数式ax2﹣2bx﹣c,当x取﹣1时,代数式的值为2,当x取0时,代数式的值为1,当x取3时,代数式的值为2,则当x取2时,代数式的值是( )A、1 B、3 C、4 D、59. 如图,已知抛物线y=x2﹣2x﹣3与x轴相交于点A,B,若在抛物线上有且只有三个不同的点C1 , C2 , C3 , 使得△ABC1 , △ABC2 , △ABC3的面积都等于a,则a的值是( )
A、 B、 C、 D、6. 下列选项中,可以用来证明命题“若a2>b2 , 则a>b“是假命题的反例是( )A、a=﹣2,b=1 B、a=3,b=﹣2 C、a=0,b=1 D、a=2,b=17. 甲,乙工程队分别承接600米,800米的道路修建工程,已知乙比甲每天多修建12米,结果甲比乙提早1天完成,问甲每天修建多少米?设甲每天修建x米,根据题意可列出方程是( )A、 = ﹣1 B、 = +1 C、 = ﹣1 D、 = +18. 对于代数式ax2﹣2bx﹣c,当x取﹣1时,代数式的值为2,当x取0时,代数式的值为1,当x取3时,代数式的值为2,则当x取2时,代数式的值是( )A、1 B、3 C、4 D、59. 如图,已知抛物线y=x2﹣2x﹣3与x轴相交于点A,B,若在抛物线上有且只有三个不同的点C1 , C2 , C3 , 使得△ABC1 , △ABC2 , △ABC3的面积都等于a,则a的值是( )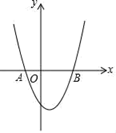 A、6 B、8 C、12 D、1610. 如图,AB,BC是⊙O的弦,∠B=60°,点O在∠B内,点D为 上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是( )
A、6 B、8 C、12 D、1610. 如图,AB,BC是⊙O的弦,∠B=60°,点O在∠B内,点D为 上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是( )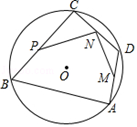 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
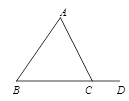
11. 因式分解:x2﹣2x= .12. 如图,∠ACD是△ABC的外角,若∠B=50°,∠ACD=120°,则∠A=.
 13. 某市号召居民节约用水,为了解居民用水情况,随机抽查了20户家庭某月的用水量,结果如下表:
13. 某市号召居民节约用水,为了解居民用水情况,随机抽查了20户家庭某月的用水量,结果如下表:户数
8
6
6
用水量(吨)
4
6
7
则这20户家庭的该月平均用水量为吨.
14. 已知扇形的圆心角为120°,弧长为4π,则扇形的面积是.15. 如图,点A是反比例函数y= 图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y= 的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=.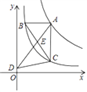 16. 如图,四边形ABCD是矩形,AD=5,AB= ,点E在CD边上,DE=2,连接BE,F是BE边上的一点,过点F作FG⊥AB于G,连接DG,将△ADG沿DG翻折的△PDG,设EF=x,当P落在△EBC内部时(包括边界),x的取值范围是.
16. 如图,四边形ABCD是矩形,AD=5,AB= ,点E在CD边上,DE=2,连接BE,F是BE边上的一点,过点F作FG⊥AB于G,连接DG,将△ADG沿DG翻折的△PDG,设EF=x,当P落在△EBC内部时(包括边界),x的取值范围是.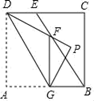
三、解答题
-
17.(1)、计算: +( )﹣1﹣|﹣3|(2)、先化简,再求值:(a﹣2)(a+2)﹣a(a﹣1),其中a=﹣118. 如图,在Rt△ABC中,∠BAC=90°,AD平分∠BAC,过AC的中点E作FG∥AD,交BA的延长线于点F,交BC于点G,
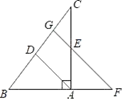 (1)、求证:AE=AF;(2)、若BC= AB,AF=3,求BC的长.19. 学了统计知识后,小红就本班同学上学“喜欢的出行方式”进行了一次调查,图(1)和图(2)是她根据采集的数据绘制的两幅不完整的统计图,请根据图中提供的信息解答以下问题:
(1)、求证:AE=AF;(2)、若BC= AB,AF=3,求BC的长.19. 学了统计知识后,小红就本班同学上学“喜欢的出行方式”进行了一次调查,图(1)和图(2)是她根据采集的数据绘制的两幅不完整的统计图,请根据图中提供的信息解答以下问题: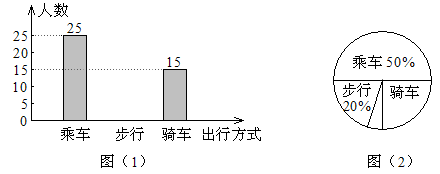 (1)、补全条形统计图,并计算出“骑车”部分所对应的圆心角的度数.(2)、若由3名“喜欢乘车”的学生,1名“喜欢骑车”的学生组队参加一项活动,现欲从中选出2人担任组长(不分正副),求出2人都是“喜欢乘车”的学生的概率,(要求列表或画树状图)20. 在直角坐标系中,我们把横,纵坐标都是整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,4),B(1,1),请在所给网格区域(含边界)上按要求画整点三角形.
(1)、补全条形统计图,并计算出“骑车”部分所对应的圆心角的度数.(2)、若由3名“喜欢乘车”的学生,1名“喜欢骑车”的学生组队参加一项活动,现欲从中选出2人担任组长(不分正副),求出2人都是“喜欢乘车”的学生的概率,(要求列表或画树状图)20. 在直角坐标系中,我们把横,纵坐标都是整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,4),B(1,1),请在所给网格区域(含边界)上按要求画整点三角形.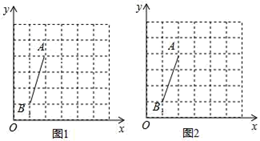
①在图1中画一个Rt△PAB,使点P落在坐标轴上;
②在图2中画一个等腰△PAB,使得△PAB的面积为4.
21. 如图,▱ABCD与抛物线y=﹣x2+bx+c相交于点A,B,D,点C在抛物线的对称轴上,已知点B(﹣1,0),BC=4.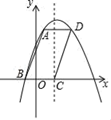 (1)、求抛物线的解析式;(2)、求BD的函数表达式.22. 如图,在⊙O中,半径OD⊥直径AB,CD与⊙O相切于点D,连接AC交⊙O于点E,交OD于点G,连接CB并延长交⊙于点F,连接AD,EF.
(1)、求抛物线的解析式;(2)、求BD的函数表达式.22. 如图,在⊙O中,半径OD⊥直径AB,CD与⊙O相切于点D,连接AC交⊙O于点E,交OD于点G,连接CB并延长交⊙于点F,连接AD,EF.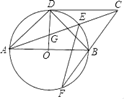 (1)、求证:∠ACD=∠F;(2)、若tan∠F=
(1)、求证:∠ACD=∠F;(2)、若tan∠F=①求证:四边形ABCD是平行四边形;
②连接DE,当⊙O的半径为3时,求DE的长.
23. 小王准备给家中长为3米的正方形ABCD电视墙铺设大理石,按图中所示的方案分成9块区域分别铺设甲,乙,丙三种大理石(正方形EFGH是由四块全等的直角三角形围成),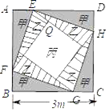 (1)、已知甲大理石的单价为150元/m2 , 乙大理石的单价为200元/m2 , 丙大理石的单价为300元/m2 , 整个电视墙大理石总价为1700元.
(1)、已知甲大理石的单价为150元/m2 , 乙大理石的单价为200元/m2 , 丙大理石的单价为300元/m2 , 整个电视墙大理石总价为1700元.①当铺设甲,乙大理石区域面积相等时,求铺设丙大理石区域的面积.
②设铺设甲,乙大理石区域面积分别为xm2 , ym2 , 当丙的面积不低于1m2时,求出y关于x的函数关系式,并写出y的最大值.
(2)、若要求AE:AF=1:2,EQ:FQ=1:3,甲,乙大理石单价之和为300元/m2 , 丙大理石的单价不低于300元/m2 , 铺设三种大理石总价为1620元,求甲的单价取值范围.24. 如图在矩形ABCD中,AB=8,过对角线AC的中点O作直线PE,交AB于点P,交CD于点Q,交射线AD于点E,连接CE,作点Q关于CE对称的对称点Q′,以Q′为圆心,为CQ′半径作⊙Q′,交CE于点M,设BC=x.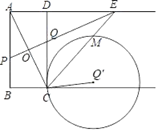 (1)、请说明△AOP≌△COQ的理由.(2)、若AP=5,
(1)、请说明△AOP≌△COQ的理由.(2)、若AP=5,①请用x的代数式表示DE的长.
②当△DQM为直角三角形时,请求出所有满足条件的BC的值.
(3)、若存在⊙Q′同时与直线AC和直线AD相切,请直接写出⊙Q′的半径.