浙江省台州市温岭市、天台县2019届数学中考一模试卷
试卷更新日期:2019-09-03 类型:中考模拟
一、单选题
-
1. 下列四个几何体中,主视图是三角形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数,如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为( )
2. 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数,如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为( )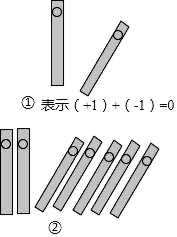 A、﹣1 B、﹣2 C、﹣3 D、﹣43. 下列计算正确的是( )A、a3+a4=a7 B、a4•a5=a9 C、4m•5m=9m D、a3+a3=2a64. 测试五位学生的“一分钟跳绳”成绩,得到五个各不相同的数据,在统计时出现了一处错误:将最高成绩写得更高了,则计算结果不受影响的是( )A、中位数 B、平均数 C、方差 D、极差5. 不等式4﹣2x≥0的解集在数轴上表示为( )A、
A、﹣1 B、﹣2 C、﹣3 D、﹣43. 下列计算正确的是( )A、a3+a4=a7 B、a4•a5=a9 C、4m•5m=9m D、a3+a3=2a64. 测试五位学生的“一分钟跳绳”成绩,得到五个各不相同的数据,在统计时出现了一处错误:将最高成绩写得更高了,则计算结果不受影响的是( )A、中位数 B、平均数 C、方差 D、极差5. 不等式4﹣2x≥0的解集在数轴上表示为( )A、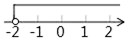 B、
B、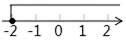 C、
C、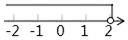 D、
D、 6. 将抛物线y=x2﹣2x﹣3沿x轴折得到的新抛物线的解析式为( )A、y=﹣x2+2x+3 B、y=﹣x2﹣2x﹣3 C、y=x2+2x﹣3 D、y=x2﹣2x+37. 如图,在△ABC中,点D是AB边上的一点,若∠ACD=∠ B.AD=1,AC=2,△ADC的面积为S,则△BCD的面积为( )
6. 将抛物线y=x2﹣2x﹣3沿x轴折得到的新抛物线的解析式为( )A、y=﹣x2+2x+3 B、y=﹣x2﹣2x﹣3 C、y=x2+2x﹣3 D、y=x2﹣2x+37. 如图,在△ABC中,点D是AB边上的一点,若∠ACD=∠ B.AD=1,AC=2,△ADC的面积为S,则△BCD的面积为( )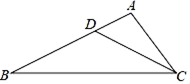 A、S B、2S C、3S D、4S8. 如图,锐角△ABC中,BC>AB>AC,求作一点P,使得∠BPC与∠A互补,甲、乙两人作法分别如下:
A、S B、2S C、3S D、4S8. 如图,锐角△ABC中,BC>AB>AC,求作一点P,使得∠BPC与∠A互补,甲、乙两人作法分别如下: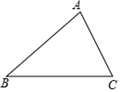
甲:以B为圆心,AB长为半径画弧交AC于P点,则P即为所求.
乙:作BC的垂直平分线和∠BAC的平分线,两线交于P点,则P即为所求.
对于甲、乙两人的作法,下列叙述正确的是( )
A、两人皆正确 B、甲正确,乙错误 C、甲错误,乙正确 D、两人皆错误二、填空题
-
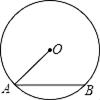
9. 如图,AB是⊙O的弦,半径OA=5,sinA= ,则弦AB的长为.
 10. 一项工程,先由甲独做,后乙加入合作直至完成,工程剩余工作量y与甲工作时间x(天)的函数关系如图所示,若要使工程提前4天完成,那么乙应该在甲工作第天后加入合作.
10. 一项工程,先由甲独做,后乙加入合作直至完成,工程剩余工作量y与甲工作时间x(天)的函数关系如图所示,若要使工程提前4天完成,那么乙应该在甲工作第天后加入合作.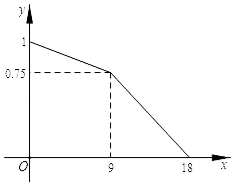 11. 因式分解:a2﹣4= .12. 将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置,如果∠CDE=40°,那么∠CAF的大小为.
11. 因式分解:a2﹣4= .12. 将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置,如果∠CDE=40°,那么∠CAF的大小为.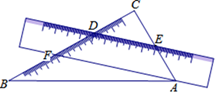 13. 在一个不透明的盒子里有20个除颜色外均相同的小球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复实验后,发现摸到红球的频率稳定在0.4,由此估计盒子中红球的个数为.
13. 在一个不透明的盒子里有20个除颜色外均相同的小球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复实验后,发现摸到红球的频率稳定在0.4,由此估计盒子中红球的个数为. 14. 如图,先将边长为6m的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△AB′C′,当两个三角形重叠部分的面积为8cm2时,它移动的距离AA′等于cm.
14. 如图,先将边长为6m的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△AB′C′,当两个三角形重叠部分的面积为8cm2时,它移动的距离AA′等于cm.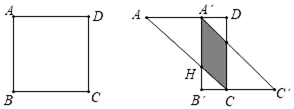 15. 如图是反比例函数 和 在第一象限的图象,在 上取点M,分别作两坐标轴的垂线交 于点A、B,连按OA、OB,则图中阴影部分面积为.
15. 如图是反比例函数 和 在第一象限的图象,在 上取点M,分别作两坐标轴的垂线交 于点A、B,连按OA、OB,则图中阴影部分面积为.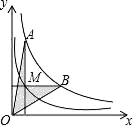 16. 在矩形ABCD中,AB=3,BC=4,点E、F分别在BC与CD上,且∠EAF=45°.如图甲,若EA=EF,则EF=;如图乙,若CE=CF,则EF=.
16. 在矩形ABCD中,AB=3,BC=4,点E、F分别在BC与CD上,且∠EAF=45°.如图甲,若EA=EF,则EF=;如图乙,若CE=CF,则EF=.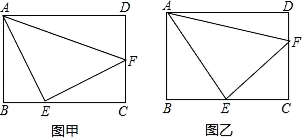
三、解答题
-
17.(1)、计算: ;(2)、化简:﹣2(a﹣3)+(a+1)218. 如图,已知D、E两点在线段BC上,AB=AC,AD=AE.证明:BD=CE.
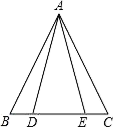 19. 某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆;两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计,EF长度远大于车辆宽度),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,该地下车库出口的车辆限高标志牌设置如图4是否合理?请通过计算说明理由.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
19. 某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆;两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计,EF长度远大于车辆宽度),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,该地下车库出口的车辆限高标志牌设置如图4是否合理?请通过计算说明理由.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) 20. 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E
20. 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E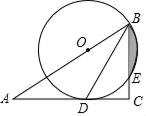 (1)、求证:AC是⊙O的切线;(2)、若OB=2,CD= ,求图中阴影部分的面积(结果保留 ).21. 从共享单车,共享汽车等共享出行到共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速的普及,根据国家信息中心发布的中国分享经济发展报告2017显示,参与共享经济活动超6亿人,比上一年增加约1亿人.
(1)、求证:AC是⊙O的切线;(2)、若OB=2,CD= ,求图中阴影部分的面积(结果保留 ).21. 从共享单车,共享汽车等共享出行到共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速的普及,根据国家信息中心发布的中国分享经济发展报告2017显示,参与共享经济活动超6亿人,比上一年增加约1亿人.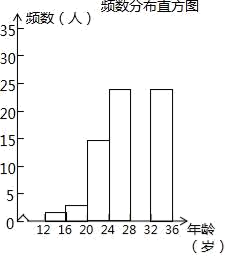 (1)、为获得北京市市民参与共享经济活动信息,下列调查方式中比较合理的是 ;A、对某学校的全体同学进行问卷调查 B、对某小区的住户进行问卷调查 C、在全市里的不同区县,选取部分市民进行问卷调查(2)、调查小组随机调查了延庆区市民骑共享单车情况,某社区年龄在12~36岁的人有1000人,从中随机抽取了100人,统计了他们骑共享单车的人数,并绘制了如下不完整的统计图表.如图所示.骑共享单车的人数统计表
(1)、为获得北京市市民参与共享经济活动信息,下列调查方式中比较合理的是 ;A、对某学校的全体同学进行问卷调查 B、对某小区的住户进行问卷调查 C、在全市里的不同区县,选取部分市民进行问卷调查(2)、调查小组随机调查了延庆区市民骑共享单车情况,某社区年龄在12~36岁的人有1000人,从中随机抽取了100人,统计了他们骑共享单车的人数,并绘制了如下不完整的统计图表.如图所示.骑共享单车的人数统计表年龄段(岁)
频数
频率
12≤x<16
2
0.02
16≤x<20
3
0.03
20≤x<24
15
a
24≤x<28
25
0.25
28≤x<32
b
0.30
32≤x<36
25
0.25
根据以上信息解答下列问题:
①统计表中的a=;b=;
②补全频数分布直方图;
③试估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有多少人?
22. 某水果店计划购进甲、乙两种新出产的水果共140千克,这两种水果的进价、售价如表所示:进价(元/千克)
售价(元/千克)
甲种
5
8
乙种
9
13
(1)、若该水果店预计进货款为1000元,则这两种水果各购进多少千克?(2)、若该水果店决定乙种水果的进货量不超过甲种水果的进货量的3倍,应怎样安排进货才能使水果店在销售完这批水果时获利最多?此时利润为多少元?23. 如图1,AB是曲线,BC是线段,点P从点A出发以不变的速度沿A﹣B﹣C运动,到终点C停止,过点P分别作x轴、y轴的垂线分别交x轴、y轴于点M、点N,设矩形MONP的面积为S运动时间为(秒),S与t的函数关系如图2所示,(FD为平行x轴的线段)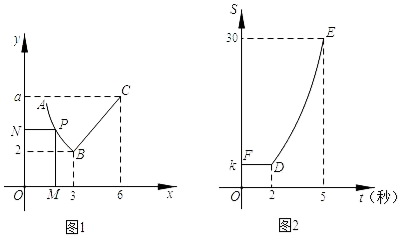 (1)、直接写出k、a的值.(2)、求曲线AB的长l.(3)、求当2≤t≤5时关于的函数解析式.24. 如图1,平面内有一点P到△ABC的三个顶点的距离分别为PA、PB、PC,若有PA2=PB2+PC2则称点P为△ABC关于点A的勾股点.
(1)、直接写出k、a的值.(2)、求曲线AB的长l.(3)、求当2≤t≤5时关于的函数解析式.24. 如图1,平面内有一点P到△ABC的三个顶点的距离分别为PA、PB、PC,若有PA2=PB2+PC2则称点P为△ABC关于点A的勾股点. (1)、如图2,在4×5的网格中,每个小正方形的长均为1,点A、B、C、D、E、F、G均在小正方形的顶点上,则点D是△ABC关于点的勾股点;在点E、F、G三点中只有点是△ABC关于点A的勾股点.(2)、如图3,E是矩形ABCD内一点,且点C是△ABE关于点A的勾股点,
(1)、如图2,在4×5的网格中,每个小正方形的长均为1,点A、B、C、D、E、F、G均在小正方形的顶点上,则点D是△ABC关于点的勾股点;在点E、F、G三点中只有点是△ABC关于点A的勾股点.(2)、如图3,E是矩形ABCD内一点,且点C是△ABE关于点A的勾股点,①求证:CE=CD;
②若DA=DE,∠AEC=120°,求∠ADE的度数.
(3)、矩形ABCD中,AB=5,BC=6,E是矩形ABCD内一点,且点C是△ABE关于点A的勾股点,①若△ADE是等腰三角形,求AE的长;
②直接写出AE+ BE的最小值.