浙江省绍兴市诸暨市浣江教育集团2019届数学中考模拟试卷（3月）

试卷更新日期：2019-09-03 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣3的倒数是（）

A、﹣3 B、3 C、﹣ $\frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 统计数据显示，2018年绍兴市进出口贸易总额达2200亿元，其中2200亿元用科学记数法表示为（）

A、2.2×10³元 B、22×10⁸元 C、2.2×10¹¹元 D、0.22×10¹²元

查看试题解析
3. 下图中几何体的主视图是（）.

A、 B、 C、 D、

查看试题解析
4. 下列运算正确的是（）

A、a²+a³=a⁵ B、a（b﹣1）=ab﹣a C、3a^﹣¹= $\frac{1}{3 a}$ D、（3a²﹣6a+3）÷3=a²﹣2a

查看试题解析
5. 如图，已知圆心角∠AOB=110°，则圆周角∠ACB=（）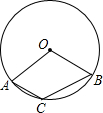

A、55° B、110° C、120° D、125°

查看试题解析
6. 浙江广厦篮球队5名场上队员的身高（单位：cm）是：184，188，190，192，194.现用一名身高为170cm的队员换下场上身高为190cm的队员，与换人前相比，场上队员的身高（）

A、平均数变小，方差变小 B、平均数变小，方差变大 C、平均数变大，方差变小 D、平均数变大，方差变大

查看试题解析
7. 在△ABC中，若O为BC边的中点，则必有：AB²+AC²=2AO²+2BO²成立.依据以上结论，解决如下问题：如图，在矩形DEFG中，已知DE=4，EF=3，点P在以DE为直径的半圆上运动，则PF²+PG²的最小值为（）

A、 $\sqrt{10}$ B、 $\frac{19}{2}$ C、34 D、10

查看试题解析
8. 将抛物线y＝2x²﹣1沿直线y＝2x方向向右上方平移2 $\sqrt{5}$ 个单位，得到新抛物线的解析式为（）

A、y＝2（x+2）²+3 B、 $y = 2 {(x - 2 \sqrt{5})}^{2} - 1$ C、 $y = 2 x^{2} + 2 \sqrt{5} - 1$ D、y＝2（x﹣2）²+3

查看试题解析
9. 如图，在平面直角坐标系中，矩形ABCD的面积为定值，它的对称中心恰与原点重合，且AB∥y轴，CD交x轴于点M，过原点的直线EF分别交AD、BC边于点E、F，以EF为一边作矩形EFGH，并使EF的对边GH所在直线过点M，若点A的横坐标逐渐增大，图中矩形EFGH的面积的大小变化情况是（）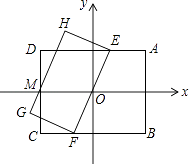

A、一直减小 B、一直不变 C、先减小后增大 D、先增大后减小

查看试题解析
10. 某届世界杯的小组比赛规则：四个球队进行单循环比赛（每两队赛一场），胜一场得3分，平一场得1分，负一场得0分，某小组比赛结束后，甲、乙，丙、丁四队分别获得第一，二，三，四名，各队的总得分恰好是四个连续奇数，则与乙打平的球队是（）

A、甲 B、甲与丁 C、丙 D、丙与丁

查看试题解析

二、填空题

11. 分解因式：ab²﹣9a= ．

查看试题解析
12. 在学校组织的游艺晚会上，掷飞镖游艺区游戏区规则如下，如图掷到A区和B区的得分不同，A区为小圆内部分，B区为大圆内小圆外部分（掷中一次记一个点）现统计小华、小明和小芳掷中与得分情况，如图所示，依此方法计算小芳的得分为.

查看试题解析
13. 如图，五边形ABCDE是正五边形.若l₁∥l₂ ，则∠1－∠2＝°.

查看试题解析
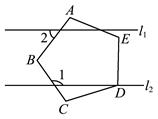14. 某景区修建一栋复古建筑，其窗户设计如图所示.圆O的圆心与矩形ABCD对角线的交点重合，且圆与矩形上下两边相切（E为上切点），与左右两边相交（F，G为其中两个交点），图中阴影部分为不透光区域，其余部分为透光区域.已知圆的半径为1m，根据设计要求，若∠EOF=45°，则此窗户的透光率（透光区域与矩形窗面的面积的比值）为.

查看试题解析
15. 如图，Rt△ABC中，∠C＝90°，AC＝3，BC＝4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN，四块阴影部分的面积分别为S₁、S₂、S₃、S₄.则S₁﹣S₂+S₃+S₄等于.

查看试题解析
16. 如图，将一块直角三角板OAB放在平面直角坐标系中，B（2，0），∠AOB=60°，点A在第一象限，过点A的双曲线为y= $\frac{k}{x}$ ，在x轴上取一点P，过点P作直线OA的垂线l，以直线l为对称轴，线段OB经轴对称变换后的像是O′B′.设P（t，0）当O′B′与双曲线有交点时，t的取值范围是.

查看试题解析

三、解答题

17.

(1)、计算 $2 \cos 45^{°} + {(\frac{1}{3})}^{- 1} + {(\sqrt{3} - 1)}^{0} - | 1 - \sqrt{2} |$

(2)、解分式方程： $\frac{x}{x - 7} - \frac{1}{7 - x}$ ＝2

查看试题解析
18. 今年我市将创建全国森林城市，提出了“共建绿色城”的倡议.某校积极响应，在3月12日植树节这天组织全校学生开展了植树活动，校团委对全校各班的植树情况道行了统计，绘制了如图所示的两个不完整的统计图.

(1)、求该校的班级总数；

(2)、将条形统计图补充完整；

(3)、求该校各班在这一活动中植树的平均数.

查看试题解析
19. 如图，已知点 $D$ 在反比例函数 $y = \frac{a}{x}$ 的图象上，过点 $D$ 作 $D B ⊥ y$ 轴，垂足为 $B (0 ， 3)$ ，直线 $y = k x + b$ 经过点 $A (5 ， 0)$ ，与 $y$ 轴交于点 $C$ ，且 $B D = O C$ ， $O C ： O A = 2 ： 5$ .

(1)、求反比例函数 $y = \frac{a}{x}$ 和一次函数 $y = k x + b$ 的表达式；

(2)、直接写出关于 $x$ 的不等式 $\frac{a}{x} > k x + b$ 的解集.

查看试题解析
20. 如图，在方格纸中，点A，B，P，Q都在格点上.请按要求画出以AB为边的格点四边形.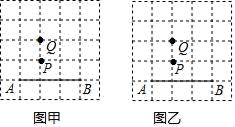

(1)、在图甲中画出一个▱ABCD，使得点P为▱ABCD的对称中心；

(2)、在图乙中画出一个▱ABCD，使得点P，Q都在▱ABCD的对角线上.

查看试题解析
21. 为营造“安全出行”的良好交通氛围，实时监控道路交迸，某市交管部门在路口安装的高清摄像头如图所示，立杆MA与地面AB垂直，斜拉杆CD与AM交于点C，横杆DE∥AB，摄像头EF⊥DE于点E，AC=55米，CD=3米，EF=0.4米，∠CDE=162°。

(1)、求∠MCD的度数；

(2)、求摄像头下端点F到地面AB的距离。(精确到百分位)
（参考数据；sin72°=0.95，cos72°≈0.31，tan72°=3.08，sin18°≈0.31，cos18°≈0.95，tan18°≈0.32）

查看试题解析
22. 对任意一个三位数n，如果n满足各个数位上的数字互不相同，且都不为零，那么称这个数为“相异数”，将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数，把这三个新三位数的和与111的商记为F（n）.例如n＝123，对调百位与十位上的数字得到213，对调百位与个位上的数字得到321，对调十位与个位上的数字得到132，这三个新三位数的和为213+321+132＝666，666÷111＝6，所以F（123）＝6.

(1)、计算：F（143），F（624）；

(2)、若m是“相异数”，m的百位上的数字为7，十位上的数字比个位上的数字多3，且F（m）＝22，“相异数”m是多少？

(3)、若s，t都是“相异数”，其中s＝100a+35，t＝160+b（1≤a≤9，1≤b≤9，a，b都是正整数），当F（s）+F（t）＝22时，求a+b的值.

查看试题解析
23. 菱形ABCD中、∠BAD＝120°，点O为射线CA 上的动点，作射线OM与直线BC相交于点E，将射线OM绕点O逆时针旋转60°，得到射线ON，射线ON与直线CD相交于点F．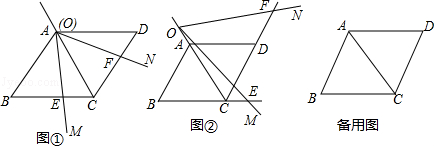

(1)、如图①，点O与点A重合时，点E，F分别在线段BC，CD上，请直接写出CE，CF，CA三条段段之间的数量关系；

(2)、如图②，点O在CA的延长线上，且OA＝ $\frac{1}{3}$ AC，E，F分别在线段BC的延长线和线段CD的延长线上，请写出CE，CF，CA三条线段之间的数量关系，并说明理由；

(3)、点O在线段AC上，若AB＝6，BO＝2 $\sqrt{7}$ ，当CF＝1时，请直接写出BE的长．

查看试题解析
24. 如图①，直线 $l$ 表示一条东西走向的笔直公路，四边形ABCD是一块边长为100米的正方形草地，点A，D在直线 $l$ 上，小明从点A出发，沿公路 $l$ 向西走了若干米后到达点E处，然后转身沿射线EB方向走到点F处，接着又改变方向沿射线FC方向走到公路 $l$ 上的点G处，最后沿公路 $l$ 回到点A处.设AE=x米
(其中x>0)，GA=y米，已知y与x之间的函数关系如图②所示，

(1)、求图②中线段MN所在直线的函数表达式；

(2)、试问小明从起点A出发直至最后回到点A处，所走过的路径(即△EFG)是否可以是一个等腰三角形？如果可以，求出相应x的值；如果不可以，说明理由.

查看试题解析