浙江省绍兴市上虞区2019届数学中考一模试卷
试卷更新日期:2019-09-03 类型:中考模拟
一、单选题
-
1. 3的相反数是( )A、﹣3 B、3 C、 D、2. 据国家外汇管理局4月7日公布的数据显示,截至2019年3月末,我国外汇储备规模为30988亿美元将30988亿用科学记数法表示为( )A、30988×108 B、3.0988×1012 C、3.0988×1011 D、3.0988×10133. 有4个相同的立方体搭成的几何体如图所示,则它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 有6张扑克牌(如图),背面朝上,从中任抽一张,则抽到方块牌的概率是( )
4. 有6张扑克牌(如图),背面朝上,从中任抽一张,则抽到方块牌的概率是( ) A、 B、 C、 D、5. 下列从左到右的恒等变形中,变形依据与其它三项不同的是( )A、 B、2(x﹣y)=2x﹣2y C、 D、a(b﹣1)=ab﹣a6. 为了说明各种三角形之间的关系,小敏画了如下的结构图(如图1).小聪为了说明“A.正方形;B.矩形;C.四边形;D.菱形;E.平行四边形”这五个概念之间的关系,类比小敏的思路,画了如下结构图(如图2),则在用“①、②、③、④”所标注的各区域中,正确的填法依次是( )(用名称前的字母代号表示)
A、 B、 C、 D、5. 下列从左到右的恒等变形中,变形依据与其它三项不同的是( )A、 B、2(x﹣y)=2x﹣2y C、 D、a(b﹣1)=ab﹣a6. 为了说明各种三角形之间的关系,小敏画了如下的结构图(如图1).小聪为了说明“A.正方形;B.矩形;C.四边形;D.菱形;E.平行四边形”这五个概念之间的关系,类比小敏的思路,画了如下结构图(如图2),则在用“①、②、③、④”所标注的各区域中,正确的填法依次是( )(用名称前的字母代号表示) A、C,E,B,D B、E,C,B,D C、E,C,D,B D、E,D,C,B7. 如图,在边长为1的小正方形网格中,点A,B,C,D都在这些小正方形上,AB与CD相交于点O,则tan∠AOD等于( )
A、C,E,B,D B、E,C,B,D C、E,C,D,B D、E,D,C,B7. 如图,在边长为1的小正方形网格中,点A,B,C,D都在这些小正方形上,AB与CD相交于点O,则tan∠AOD等于( ) A、 B、2 C、1 D、8. 将两个底边相等的等腰三角形按照如图所示的方式拼接在一起(隐藏互相重合的底边)的图形俗称为“筝形”.假如“筝形”下个定义,那么下面四种说法中,你认为最能够描述“筝形”特征的是( )
A、 B、2 C、1 D、8. 将两个底边相等的等腰三角形按照如图所示的方式拼接在一起(隐藏互相重合的底边)的图形俗称为“筝形”.假如“筝形”下个定义,那么下面四种说法中,你认为最能够描述“筝形”特征的是( ) A、有两组邻边相等的四边形称为“筝形” B、有两组对角分别相等的四边形称为“筝形” C、两条对角线互相垂直的四边形称为“筝形” D、以一条对角线所在直线为对称轴的四边形称为“筝形”9. 对于不为零的两个实数m,n,我们定义:m⊗n= ,那么函数y=x⊗3的图象大致是( )A、
A、有两组邻边相等的四边形称为“筝形” B、有两组对角分别相等的四边形称为“筝形” C、两条对角线互相垂直的四边形称为“筝形” D、以一条对角线所在直线为对称轴的四边形称为“筝形”9. 对于不为零的两个实数m,n,我们定义:m⊗n= ,那么函数y=x⊗3的图象大致是( )A、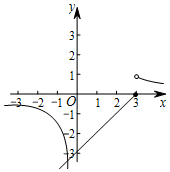 B、
B、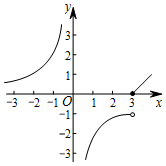 C、
C、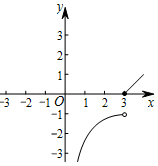 D、
D、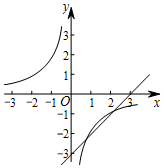 10. 在△ABC中,D是BC延长线上一点,且BC=m•BD,过D点作直线AB,AC的垂线,垂足分别为E、F,若AB=n•AC.则 =( )A、 B、 C、 D、
10. 在△ABC中,D是BC延长线上一点,且BC=m•BD,过D点作直线AB,AC的垂线,垂足分别为E、F,若AB=n•AC.则 =( )A、 B、 C、 D、二、填空题
-
11. 分解因式:4a2﹣b2= .12. 《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,不足三.问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出5钱,还差45钱:若每人出7钱,还差3钱.则合伙人数为人;羊价为钱.13. 如图,矩形ABCD中,AB=2,点E在AD边上,以E为圆心,EA长为半径的⊙E与BC相切,交CD于点F,连接EF.若扇形EAF的面积为 ,则BC的长是.
 14. 已知直线l和直线l外一点A,以点A为圆心,适当的长度为半径作弧交直线l于点M,N,再分别以M,N为圆心,大于 MN长为半径作弧,两弧交于点P(点P与点A在直线l的两侧),连结PM,作直线PA交MN于点O,若PO= ,MN=2,则cos∠APM=.15. 如图,在平面直角坐标系xOy中,点P坐标为(1, ),以OP为斜边作等腰直角△OAP,直角顶点A在反比例函数y= 的图象上,则k的值是.
14. 已知直线l和直线l外一点A,以点A为圆心,适当的长度为半径作弧交直线l于点M,N,再分别以M,N为圆心,大于 MN长为半径作弧,两弧交于点P(点P与点A在直线l的两侧),连结PM,作直线PA交MN于点O,若PO= ,MN=2,则cos∠APM=.15. 如图,在平面直角坐标系xOy中,点P坐标为(1, ),以OP为斜边作等腰直角△OAP,直角顶点A在反比例函数y= 的图象上,则k的值是.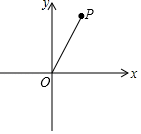 16. 如图,已知△ABC,△DEF均为等腰直角三角形,EF=10 ,顶点D,E分别在边AB,AC上滑动.则在滑动过程中,点A,F间距离的最大值为.
16. 如图,已知△ABC,△DEF均为等腰直角三角形,EF=10 ,顶点D,E分别在边AB,AC上滑动.则在滑动过程中,点A,F间距离的最大值为.
三、解答题
-
17.(1)、计算:(2)、解不等式:18. “腹有诗书气自华,阅读路伴我成长”,我区某校学生会以“每天阅读1小时”为问卷主题,对学生最喜爱的书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅末完成的统计图,请根据图1和图2提供的信息,解答下列问题:
 (1)、把折线统计图(图1)补充完整;(2)、该校共有学生1200名,请估算最喜爱科普类书籍的学生人数.19. 如图是某种品牌的篮球架实物图与示意图,已知底座BC=0.6米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.5米,篮板顶端F点到篮框D的距离FD=1.4米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离.(精确到0.1米.参考数据:cos75°≈0.3,sin75°≈0.9,.tan75°≈3.7, ≈1.7, ≈1.4)
(1)、把折线统计图(图1)补充完整;(2)、该校共有学生1200名,请估算最喜爱科普类书籍的学生人数.19. 如图是某种品牌的篮球架实物图与示意图,已知底座BC=0.6米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.5米,篮板顶端F点到篮框D的距离FD=1.4米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离.(精确到0.1米.参考数据:cos75°≈0.3,sin75°≈0.9,.tan75°≈3.7, ≈1.7, ≈1.4) 20. 小敏学习之余设计了一个求函数表达式的程序,具体如图所示,则当输入下列点的坐标时,请按程序指令解答.
20. 小敏学习之余设计了一个求函数表达式的程序,具体如图所示,则当输入下列点的坐标时,请按程序指令解答. (1)、P1(1,0),P2(﹣3,0).(2)、P1(2,﹣1),P2(4,﹣3)21. 如图,公路上有A、B、C三个汽车站,一辆汽车8:00从离A站10km的P地出发,向C站匀速行驶,15min后离A站30km.
(1)、P1(1,0),P2(﹣3,0).(2)、P1(2,﹣1),P2(4,﹣3)21. 如图,公路上有A、B、C三个汽车站,一辆汽车8:00从离A站10km的P地出发,向C站匀速行驶,15min后离A站30km. (1)、设出发xh后,汽车离A站ykm,写出y与x之间的函数表达式;(2)、当汽车行驶到离A站250km的B站时,接到通知要在12:00前赶到离B站60km的C站.汽车按原速行驶,能否准时到达?如果能,那么汽车何时到达C站?22. 如图,在平行四边形ABCD中,AB= ,BC=8,∠B=60°,将平行四边形ABCD沿EF折叠,点D恰好落在边AB的中点D′处,折叠后点C的对应点为C′,D′C′交BC于点G,∠BGD′=32°.
(1)、设出发xh后,汽车离A站ykm,写出y与x之间的函数表达式;(2)、当汽车行驶到离A站250km的B站时,接到通知要在12:00前赶到离B站60km的C站.汽车按原速行驶,能否准时到达?如果能,那么汽车何时到达C站?22. 如图,在平行四边形ABCD中,AB= ,BC=8,∠B=60°,将平行四边形ABCD沿EF折叠,点D恰好落在边AB的中点D′处,折叠后点C的对应点为C′,D′C′交BC于点G,∠BGD′=32°. (1)、求∠D′EF的度数;(2)、求线段AE的长.23. 在正方形ABCD中,点M是射线BC上一点,点N是CD延长线上一点,且BM=DN,直线BD与MN交于点E.
(1)、求∠D′EF的度数;(2)、求线段AE的长.23. 在正方形ABCD中,点M是射线BC上一点,点N是CD延长线上一点,且BM=DN,直线BD与MN交于点E. (1)、如图1.当点M在BC上时,为证明“BD﹣2DE= BM”这一结论,小敏添加了辅助线:过点M作CD的平行线交BD于点P.请根据这一思路,帮助小敏完成接下去的证明过程.(2)、如图2,当点M在BC的延长线上时,则BD,DE,BM之间满足的数量关系是.(3)、在(2)的条件下,连接BN交AD于点F,连接MF交BD于点G,如图3,若 CM=2,则线段DG=.24. 在平面直角坐标系xOy中,A(t,0),B(t+ ,0),对于线段AB和点P给出如下定义:当∠APB=90°时,称点P为线段AB的“直角视点”.
(1)、如图1.当点M在BC上时,为证明“BD﹣2DE= BM”这一结论,小敏添加了辅助线:过点M作CD的平行线交BD于点P.请根据这一思路,帮助小敏完成接下去的证明过程.(2)、如图2,当点M在BC的延长线上时,则BD,DE,BM之间满足的数量关系是.(3)、在(2)的条件下,连接BN交AD于点F,连接MF交BD于点G,如图3,若 CM=2,则线段DG=.24. 在平面直角坐标系xOy中,A(t,0),B(t+ ,0),对于线段AB和点P给出如下定义:当∠APB=90°时,称点P为线段AB的“直角视点”. (1)、若t=﹣ ,在点C(0, ),D(﹣1, ),E( , )中,能够成为线段AB“直角视点”的是.(2)、直线MN分别交x轴、y轴于点M、N,点M的坐标是( ,0),∠OMN=30°.
(1)、若t=﹣ ,在点C(0, ),D(﹣1, ),E( , )中,能够成为线段AB“直角视点”的是.(2)、直线MN分别交x轴、y轴于点M、N,点M的坐标是( ,0),∠OMN=30°.①线段AB的“直角视点”P在直线MN上,且∠ABP=60°,求点P的坐标.
②在①的条件下,记Q为直线MN上的动点,在点Q的运动过程中,△QAB的周长存在最小值,试求△QAB周长的最小值.
③若线段AB的所有“直角视点”都在△MON内部,则t的取值范围是.