浙江省绍兴市2019届数学中考模拟试卷（5月)

试卷更新日期：2019-09-03 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣2019的绝对值是（）

A、2019 B、﹣2019 C、 $\frac{1}{2019}$ D、﹣ $\frac{1}{2019}$

查看试题解析
2. 习近平主席在2018年新年贺词中指出，2017年，基本医疗保险已经覆盖1350000000人．将1350000000用科学记数法表示为（）

A、135×10⁷ B、1.35×10⁹ C、13.5×10⁸ D、1.35×10¹⁴

查看试题解析
3. 下列运算正确的是（）

A、x³+x²=x⁵ B、x³﹣x²=x C、x³÷x²=x D、x³•x²=x⁶

查看试题解析
4. 在一个不透明的口袋中装有5个完全相同的小球，把它们分别标号为1，2，3，4，5，从中随机摸出一个小球，其标号是奇数的概率为（　　）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
5. 已知（m-n）²=8，（m+n）²=2，则m²+n²=（）

A、10 B、6 C、5 D、3

查看试题解析
6. 张老师出门散步时离家的距离y与时间x之间的函数图象如图所示，若用黑点表示张老师家的位置，则张老师散步行走的路线可能是（）

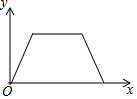A、 B、 C、 D、

查看试题解析
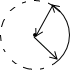7. 若抛物线y＝ax²+bx+c（a≠0）与x轴两个交点间的距离为6，称此抛物线为定弦抛物线.已知某定弦抛物线开口向上，对称轴为直线x＝2，且通过（1，y₁），（3，y₂），（﹣1，y₃），（﹣3，y₄）四点，则y₁ ， y₂ ， y₃ ， y₄中为正数的是（）

A、y₁ B、y₂ C、y₃ D、y₄

查看试题解析
8. 如图，在△ABC中，∠B＝50°，点D为边AB的中点，点E在边AC上，将△ADE沿DE折叠，使得点A恰好落在BC的延长线上的点F处，DF与AC交于点O，连结CD，则下列结论一定正确的是（）

A、CE＝EF B、∠BDF＝90° C、△EOD和△COF的面积相等 D、∠BDC＝∠CEF+∠A

查看试题解析
9. 如图，一个铁环上挂着6个分别编有号码1，2，3，4，5，6的铁片.如果把其中编号为2，4的铁片取下来，再先后把它们穿回到铁环上的仼意位置，则铁环上的铁片（无论沿铁环如何滑动）不可能排成的情形是（）

A、 B、 C、 D、

查看试题解析
10. 有6个相同的立方体搭成的几何体如图所示，则它的主视图是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 分解因式：4﹣y²＝.

查看试题解析
12. 分式方程 $\frac{2}{1 - x} + 1 = \frac{x}{1 + x}$ 的解为.

查看试题解析
13. 明代数学家程大位在其所著《直指算法统宗》一书中有如下问题：
假如井不知深，先将绳三折入井，绳长四尺；后将绳四折入井，亦长一尺.问井深及绳长各若干？

意思是：“用绳子测量井深，把绳子折成三折来量，井外余绳4尺；把绳子折成四折来量，井外余绳1尺.井深和绳长各是多少？”那么井深为尺，绳长为尺.

查看试题解析
14. 如图，在正方形ABCD中，分别以点C，D为圆心，CD长为半径画弧，两弧交于点E，∠EAB的度数是.

查看试题解析
15. 如图，在平面直角坐标系xOy中，菱形ABCD的顶点A（4，4），C（﹣2，﹣2），点B，D在反比例函数 $y = \frac{k}{x}$ 的图象上，对角线BD交AC于点M，交x轴于点N，若 $\frac{BN}{ND} = \frac{5}{3}$ ，则k的值是.

查看试题解析
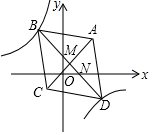16. 如图，已知∠MAN＝30°，点B在边AM上，且AB＝4 $\sqrt{3}$ ，点P从点A出发沿射线AN方向运动，在边AN上取点C（点C在点P右侧），连结BP，BC.设PC＝m，当△BPC成为等腰三角形的个数恰好有3个时，m的值为.

查看试题解析

三、解答题

17.

(1)、计算： ${(\sqrt{2019} - 1)}^{0} + \sqrt{18} \sin 45^{°} - 2^{- 2}$ .

(2)、解不等式： ${\begin{array}{l} 4 x - 3 < 5 x - 1 \\ \frac{1}{2} x - 1 ⩽ 7 - \frac{3}{2} x \end{array}$ .

查看试题解析
18. 垃圾的分类处理与回收利用，可以减少污染，节省资源.某城市环保部门为了提高宣传实效，抽样调查了部分居民小区一段时间内生活垃圾的分类情况，其相关信息如下：

根据图表解答下列问题：

(1)、请将条形统计图补充完整；

(2)、在抽样数据中，产生的有害垃圾共吨；

(3)、调查发现，在可回收物中塑料类垃圾占 $\frac{1}{5}$ ，每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5000吨，且全部分类处理，那么每月回收的塑料类垃圾可以获得多少吨二级原料？

查看试题解析
19. 如图，在8×6的方格纸中有线段AD，其中A，D在格点上，请分别按下列要求作△ABC（所作△ABC不是等腰三角形，作出一个即可.）

(1)、在图1中，作△ABC，使AD为△ABC的中线，点B，C在格点上.

(2)、在图2中，作△ABC，使AD为△ABC的高线，点B，C在格点上.

查看试题解析
20. 一辆汽车在某次行驶过程中，油箱中的剩余油量y（升）与行驶路程x（千米）之间是一次函数关系，其部分图象如图所示.

(1)、求y关于x的函数关系式；（不需要写定义域）

(2)、已知当油箱中的剩余油量为8升时，该汽车会开始提示加油，在此次行驶过程中，行驶了500千米时，司机发现离前方最近的加油站有30千米的路程，在开往该加油站的途中，汽车开始提示加油，这时离加油站的路程是多少千米？

查看试题解析
21. 如图，某人在山坡坡脚C处测得一座建筑物定点A的仰角为60°，沿山坡向上走到P处再测得该建筑物顶点A的仰角为45°.已知BC＝60m，山坡的坡比为1：2.

(1)、求该建筑物的高度（即AB的长，结果保留根号）；

(2)、求此人所在位置点P的铅直高度（即PD的长，结果保留根号）.

查看试题解析
22. 如图1，有一个“z”字图形，其中AB∥CD，AB：CD：BC＝1：2：3.

(1)、如图2，若以BC为直径的⊙O恰好经过点D，连结AO.
①求cosC.

②当AB＝2时，求AO的长.

(2)、如图3，当A，B，C，D四点恰好在同一个圆上时.求∠C的度数.

查看试题解析
23. 有一道作业题：

(1)、请你完成这道题的证明；
已知：如图1，在正方形ABCD中，G是对角线BD上一点（G与B，D不重合）连结AG，CG求证：△BAG≌△BCG

(2)、做完（1）后，小颖善于反思，她又提出了如下的问题，请你解答.
如果在射线CB上取点E，使GE＝GC，连结GE.

①如图2，当点E在线段CB上时，求证：AG⊥EG.

②探究线段AB，BE，BG之间的数量关系.

查看试题解析
24. 如图，在平面直角坐标系xOy中，已知点A（﹣3，1），点B（0，5），过点A作直线l⊥AB，过点B作BD∥l，交x轴于点D，再以点B为圆心，BD长为半径作弧，交直线l于点C（点C位于第四象限），连结BC，CD.

(1)、求线段AB的长.

(2)、点M是线段BC上一点，且BM＝CA，求DM的长.

(3)、点M是线段BC上的动点.
①若点N是线段AC上的动点，且BM＝CN，求DM+DN的最小值.

②若点N是射线AC上的动点，且BM＝CN，求DM+DN的最小值（直接写出答案）.

查看试题解析