浙江省宁波市镇海区2019届数学中考一模试卷
试卷更新日期:2019-09-03 类型:中考模拟
一、单选题
-
1. 2019的相反数是( )A、2019 B、-2019 C、 D、2. 中国企业2018年已经在“一带一路”沿线国家建立了56个经贸合作区,直接为东道国增加了20万个就业岗位,将20万用科学记数法表示应为( )A、0.2×106 B、2×105 C、20×104 D、20×1053. 在以下四个环保标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算中,正确的是( )A、 =-3 B、a3•a6=a18 C、6a6÷3a2=2a3 D、(﹣2ab2)2=2a2b45. 如图所示的物体的左视图(从左面看得到的视图)是( )
4. 下列运算中,正确的是( )A、 =-3 B、a3•a6=a18 C、6a6÷3a2=2a3 D、(﹣2ab2)2=2a2b45. 如图所示的物体的左视图(从左面看得到的视图)是( )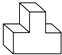 A、
A、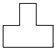 B、
B、 C、
C、 D、
D、 6. 在一个不透明的口袋里有3个红球,2个黄球,4个蓝球,这些球除颜色外全部相同,搅匀后随机从中摸出一个球,不是红球的概率是( )A、 B、 C、 D、7. 如图,直线a∥b,将含有45°的三角板ABC的直角顶点C放在直线b上,若∠1=27°,则∠2的度数是( )
6. 在一个不透明的口袋里有3个红球,2个黄球,4个蓝球,这些球除颜色外全部相同,搅匀后随机从中摸出一个球,不是红球的概率是( )A、 B、 C、 D、7. 如图,直线a∥b,将含有45°的三角板ABC的直角顶点C放在直线b上,若∠1=27°,则∠2的度数是( )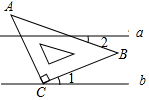 A、10° B、15° C、18° D、20°8. 如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,BO=4,则 的长为( )
A、10° B、15° C、18° D、20°8. 如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,BO=4,则 的长为( )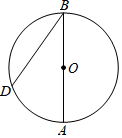 A、 B、 C、2π D、9. 如图,直线y=kx+3经过点(2,0),则关于x的不等式kx+3>0的解集是( )
A、 B、 C、2π D、9. 如图,直线y=kx+3经过点(2,0),则关于x的不等式kx+3>0的解集是( ) A、x>2 B、x<2 C、x≥2 D、x≤210. 若二次函数 的图象经过点(﹣1,0),则方程 的解为( )A、 , B、 , C、 , D、 ,11. 如图,四边形 中, , , , , , 是 的中点,则 的长为( )
A、x>2 B、x<2 C、x≥2 D、x≤210. 若二次函数 的图象经过点(﹣1,0),则方程 的解为( )A、 , B、 , C、 , D、 ,11. 如图,四边形 中, , , , , , 是 的中点,则 的长为( )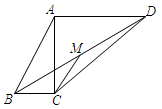 A、 B、 C、 D、12. 把六张大小形状完全相同的小平行四边形卡片(如图)放在一个底面为平行四边形的盒子底部,两种放置方法如图2、图3所示,其中3中的重叠部分是平行四边形EFGH,若EH=2GH,且图2中阴影部分的周长比图3中阴影部分的周长大3.则AB﹣AD的值为( )
A、 B、 C、 D、12. 把六张大小形状完全相同的小平行四边形卡片(如图)放在一个底面为平行四边形的盒子底部,两种放置方法如图2、图3所示,其中3中的重叠部分是平行四边形EFGH,若EH=2GH,且图2中阴影部分的周长比图3中阴影部分的周长大3.则AB﹣AD的值为( )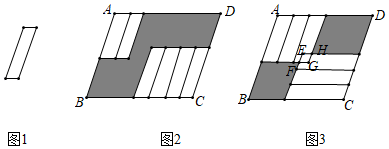 A、0.5 B、1 C、1.5 D、3
A、0.5 B、1 C、1.5 D、3二、填空题
-
13. 分解因式:2a2﹣8ab+8b2=.14. 若一组数据4,1,7,x,5的平均数为4,则这组数据的中位数为15. 如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的角为60°,此时航拍无人机与该建筑物的水平距离AD为80m,那么该建筑物的高度BC为m(结果保留根号).
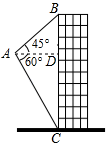 16. 如图,已知四边形ABCD是平行四边形,BC=3AB,A、B两点的坐标分别是(1,0),(0,2),C、D两点在反比例函数y= (k>0,x>0)的图象上,则k的值等于.
16. 如图,已知四边形ABCD是平行四边形,BC=3AB,A、B两点的坐标分别是(1,0),(0,2),C、D两点在反比例函数y= (k>0,x>0)的图象上,则k的值等于.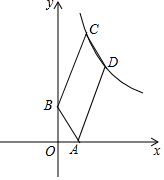 17. 如图,在菱形ABCD中,∠A=60°,M,N分别是边AB,AD上的两个点,将△AMN沿MN翻折,使A恰好与CD上的点A′重合,此时BD⊥MA′,若折痕MN= ,则菱形ABCD的面积是.
17. 如图,在菱形ABCD中,∠A=60°,M,N分别是边AB,AD上的两个点,将△AMN沿MN翻折,使A恰好与CD上的点A′重合,此时BD⊥MA′,若折痕MN= ,则菱形ABCD的面积是.
三、解答题
-
18. 先化简,再求值:(a﹣2)2+(1+a)(1﹣a),其中a=2.19. 在图1的6×6的网格中,已知格点△ABC(顶点A、B、C都在格各点上)
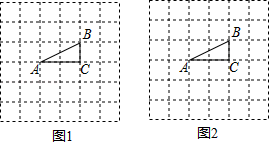
①在图1中,画出与△ABC面积相等的格点△ABD(不与△ABC全等),画出一种即可;
②在图2中,画出与△ABC相似的格点△A1B1C1(不与ABC全等),且两个三角形的对应边分别互相垂直,画出一种即可.
20. 垃圾分类处理利国利民,造子孙后代应引起社会的共同关注生活A(可回收垃圾)、B(厨余垃级)、C(有害垃圾)、D、(其他垃圾)四类进行回收处理,观某市对部分居民小区一段时间内生活垃圾的分类情况进行抽样调查,根据调查结果统计的数据,绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解决下列问题: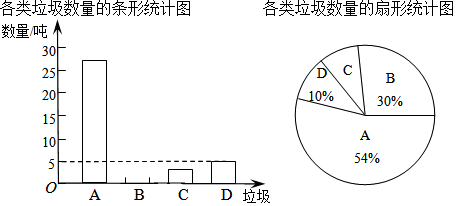 (1)、在抽样数据中,总共产生垃圾吨,其中产生的有害垃圾共吨;(2)、请将条形统计图补充完整;(3)、调查发现,在可回收垃圾中,塑料类垃圾占 ,每回收1吨塑料类垃圾可获得0.7吨二级原料,若该市每日产生的生活垃圾为5000吨,且全部分类处理,请通过计算,估计每日回收的塑料类垃圾可以获得多少吨二级原料?21. 如图,在▱ABCD中,E是对角线BD上的一点,过点C作CF∥BD,且CF=DE,连接AE,BF,EF.
(1)、在抽样数据中,总共产生垃圾吨,其中产生的有害垃圾共吨;(2)、请将条形统计图补充完整;(3)、调查发现,在可回收垃圾中,塑料类垃圾占 ,每回收1吨塑料类垃圾可获得0.7吨二级原料,若该市每日产生的生活垃圾为5000吨,且全部分类处理,请通过计算,估计每日回收的塑料类垃圾可以获得多少吨二级原料?21. 如图,在▱ABCD中,E是对角线BD上的一点,过点C作CF∥BD,且CF=DE,连接AE,BF,EF.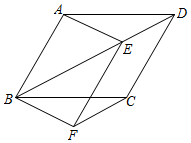 (1)、求证:△ADE≌△BCF.(2)、若∠BFC﹣∠ABE=90°,sin∠ABE= ,BF=4,求BE的长.22. 如图,正例函数y=kx(k>0)的图象与反比例函数y= (m>0,x>0)的图象交于点A,过A作AB⊥x轴于点B.已知点B的坐标为(2,0),平移直线y=kx,使其经过点B,并与y轴交于点C(0,﹣3)
(1)、求证:△ADE≌△BCF.(2)、若∠BFC﹣∠ABE=90°,sin∠ABE= ,BF=4,求BE的长.22. 如图,正例函数y=kx(k>0)的图象与反比例函数y= (m>0,x>0)的图象交于点A,过A作AB⊥x轴于点B.已知点B的坐标为(2,0),平移直线y=kx,使其经过点B,并与y轴交于点C(0,﹣3)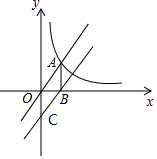 (1)、求k和m的值(2)、点M是线段OA上一点,过点M作MN∥AB,交反比例函数y= (m>0,x>0)的图象交于点N,若MN= ,求点M的坐标23. 某工厂计划招聘A、B两个工种的工人共120人,已知A、B两个工种的工人的月工费分别为2400元和3000元.(1)、若工厂每月付A、B两个工种的总工费为330000元,那么两个工种的工人各招聘多少人.(2)、若生产需要,要求B工种的人数不少于A工种人数的2倍,那么招聘A工种的人数为多少时,可使每月支付的A、B两个工种的总工资最少.24. 定义:圆心在三角形的一条边上,并与三角形的其中一边所在的直线相切的圆称为这个三角形的切圆,相切的边称为这个圆的切边
(1)、求k和m的值(2)、点M是线段OA上一点,过点M作MN∥AB,交反比例函数y= (m>0,x>0)的图象交于点N,若MN= ,求点M的坐标23. 某工厂计划招聘A、B两个工种的工人共120人,已知A、B两个工种的工人的月工费分别为2400元和3000元.(1)、若工厂每月付A、B两个工种的总工费为330000元,那么两个工种的工人各招聘多少人.(2)、若生产需要,要求B工种的人数不少于A工种人数的2倍,那么招聘A工种的人数为多少时,可使每月支付的A、B两个工种的总工资最少.24. 定义:圆心在三角形的一条边上,并与三角形的其中一边所在的直线相切的圆称为这个三角形的切圆,相切的边称为这个圆的切边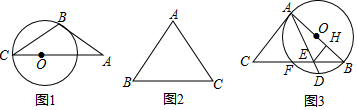 (1)、如图1,△ABC中,AB=BC,∠A=30°,点O在AC边上,以OC为半径的⊙O恰好经过点B.求证:⊙O是△ABC的切圆;(2)、如图2,△ABC中,AB=AC=10,BC=12,⊙O是△ABC的切圆,且另两条边都是⊙O的切边,求⊙O的半径;(3)、如图3,△ABC中,以AB为直径的⊙O恰好是ABC的切圆,AC是⊙O的切边,⊙O与BC交于点F,取 的中点D,连接AD交BC于点E,过点E作EH⊥AB于点H.若CF=4,BF=5,求AC和EH的长.25. 如图1,在平面直角坐标系中,抛物线与x轴交于A(﹣l,0),B(3,0)与y轴交于C(0,﹣ ).
(1)、如图1,△ABC中,AB=BC,∠A=30°,点O在AC边上,以OC为半径的⊙O恰好经过点B.求证:⊙O是△ABC的切圆;(2)、如图2,△ABC中,AB=AC=10,BC=12,⊙O是△ABC的切圆,且另两条边都是⊙O的切边,求⊙O的半径;(3)、如图3,△ABC中,以AB为直径的⊙O恰好是ABC的切圆,AC是⊙O的切边,⊙O与BC交于点F,取 的中点D,连接AD交BC于点E,过点E作EH⊥AB于点H.若CF=4,BF=5,求AC和EH的长.25. 如图1,在平面直角坐标系中,抛物线与x轴交于A(﹣l,0),B(3,0)与y轴交于C(0,﹣ ).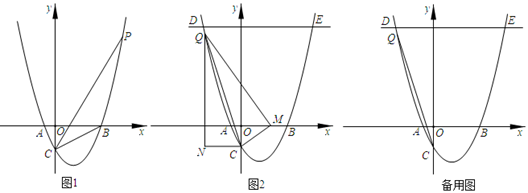 (1)、求这个抛物线的解析式;(2)、点P在(1)中的抛物线上,连结PC、BC,若∠PCB=∠OBC,求所有满足条件的点P坐标;(3)、如图2,作直线y= ,与抛物线交于D、E,连结DC,动点Q在折线C-D-E上运动,过Q作QN∥y轴,过C作CN∥x轴,直线ON、CN交于点N,将△C沿CQ折得到△QCM,若点M落在x轴上,请直接写出所有符合条件的点Q坐标。
(1)、求这个抛物线的解析式;(2)、点P在(1)中的抛物线上,连结PC、BC,若∠PCB=∠OBC,求所有满足条件的点P坐标;(3)、如图2,作直线y= ,与抛物线交于D、E,连结DC,动点Q在折线C-D-E上运动,过Q作QN∥y轴,过C作CN∥x轴,直线ON、CN交于点N,将△C沿CQ折得到△QCM,若点M落在x轴上,请直接写出所有符合条件的点Q坐标。