浙江省宁波市海曙区三校联考2019届数学中考模拟试卷(6月)
试卷更新日期:2019-09-03 类型:中考模拟
一、单选题
-
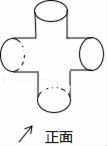
1. 下列各数为无理数的是A、2 B、 C、 D、2. 2018年国庆期间国内旅游收入5990.8亿元,将5990.8亿用科学记数法表示为( )A、 5.9908×1010 B、5.9908×1011 C、5.9908×1012 D、5.9908×1033. 下列运算中正确的是( )A、x2+x2=2x4 B、x5﹣x3=x2 C、x2•x3=x6 D、(﹣x)6÷(﹣x2)=﹣x44. 如图所示的某零件左视图是( )
 A、
A、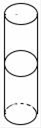 B、
B、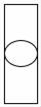 C、
C、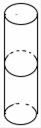 D、
D、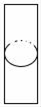 5. 从0,1,2,3,4,5,6这七个数中,随机抽取一个数,记为a,若a使关于x的不等式组 的解集为x>1,且使关于x的分式方程 =2的解为非负数,那么取到满足条件的a值的概率为( )A、 B、 C、 D、6. 如图,AB∥CD,那么( )
5. 从0,1,2,3,4,5,6这七个数中,随机抽取一个数,记为a,若a使关于x的不等式组 的解集为x>1,且使关于x的分式方程 =2的解为非负数,那么取到满足条件的a值的概率为( )A、 B、 C、 D、6. 如图,AB∥CD,那么( )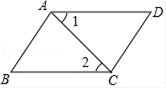 A、∠BAD与∠B互补 B、∠1=∠2 C、∠BAD与∠D互补 D、∠BCD与∠D互补7. 一元二次方程-x2+2x=0的根为( )A、 B、0,2 C、0, D、28. 如图,AD是△ABC外接圆的直径.若∠B=64°,则∠DAC等于( )
A、∠BAD与∠B互补 B、∠1=∠2 C、∠BAD与∠D互补 D、∠BCD与∠D互补7. 一元二次方程-x2+2x=0的根为( )A、 B、0,2 C、0, D、28. 如图,AD是△ABC外接圆的直径.若∠B=64°,则∠DAC等于( )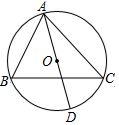 A、26° B、28° C、30° D、32°9. 某车间需加工一批零件,车间20名工人每天加工零件数如表所示:
A、26° B、28° C、30° D、32°9. 某车间需加工一批零件,车间20名工人每天加工零件数如表所示:每天加工零件数
4
5
6
7
8
人数
3
6
5
4
2
每天加工零件数的中位数和众数为( )
A、6,5 B、6,6 C、5,5 D、5,610. 如图,正方形 中, , 是 边的中点,点 是正方形内一动点, ,连接 ,将线段 绕点 逆时针旋转 得 ,连接 , .则线段 长的最小值( )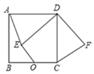 A、 B、 C、 D、11. 已知∠AOB,作图.
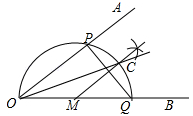
A、 B、 C、 D、11. 已知∠AOB,作图.步骤1:在OB上任取一点M,以点M为圆心,MO长为半径画半圆,分别交OA、OB于点P、Q;
步骤2:过点M作PQ的垂线交 于点C;
步骤3:画射线OC.
则下列判断:① = ;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正确的个数为( )
 A、1 B、2 C、3 D、412. 四位同学在研究函数y=ax2+bx+c(a、b、c为常数,且a≠0)时,甲发现当x=1时,函数有最大值;乙发现﹣1是方程ax2+bx+c=0的一个根;丙发现函数的最大值为﹣1;丁发现当x=2时,y=﹣2,已知四位中只有一位发现的结论时错误的,则该同学是( ).A、甲 B、乙 C、丙 D、丁
A、1 B、2 C、3 D、412. 四位同学在研究函数y=ax2+bx+c(a、b、c为常数,且a≠0)时,甲发现当x=1时,函数有最大值;乙发现﹣1是方程ax2+bx+c=0的一个根;丙发现函数的最大值为﹣1;丁发现当x=2时,y=﹣2,已知四位中只有一位发现的结论时错误的,则该同学是( ).A、甲 B、乙 C、丙 D、丁二、填空题
-
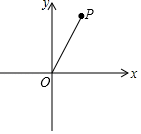
13. 分解因式:m2﹣9m=.14. 已知圆锥的底面半径为 ,母线长为 ,则它的侧面展开图的面积等于.15. 如图,在平面直角坐标系xOy中,点P坐标为(1, ),以OP为斜边作等腰直角△OAP,直角顶点A在反比例函数y= 的图象上,则k的值是.
 16. 如图,在△ABC中,DE∥AB,DE分别与AC,BC交于D,E两点.若 ,AC=3,则DC=.
16. 如图,在△ABC中,DE∥AB,DE分别与AC,BC交于D,E两点.若 ,AC=3,则DC=.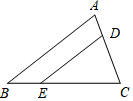 17. 如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为O.以点C为圆心,BC为半径作弧AB,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是.
17. 如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为O.以点C为圆心,BC为半径作弧AB,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是.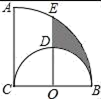 18. 如图,在菱形纸片ABCD中,AB=4,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则sin∠EFG的值为 .
18. 如图,在菱形纸片ABCD中,AB=4,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则sin∠EFG的值为 .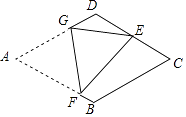
三、解答题
-
19. 先化简,再求值:( +a-2)÷ -1,其中a= +1.20. 某校“心灵信箱”的设立,为师、生之间的沟通开设了一个书面交流的渠道.为了解九年级学生对“心灵信箱”开通两年来的使用情况,某课题组对该校九年级全体学生进行了一次问卷调查,并根据调查结果绘制了如下尚不完整的统计图.
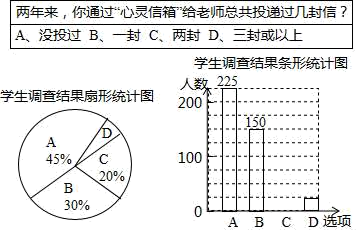
根据图表,解答以下问题:
(1)、该校九年级学生共有人;(2)、学生调查结果扇形统计图中,扇形D的圆心角度数是;(3)、请你补充条形统计图;(4)、根据调查结果可以推断:两年来,该校九年级学生通过“心灵信箱”投递出的信件总数至少有封.21. 图①、图②均为3×3的正方形网格,每个小正方形的边长都为1,请在图①、图②中各画一个顶点在格点的三角形.
要求:(1)所画的三角形为钝角三角形;(2)所画的三角形三边中有一边长是另一边长的 倍;(3)图①、图②中所画的三角形不全等.
22. 如图,已知反比例函数y= (k≠0)的图象过点A(-3,2).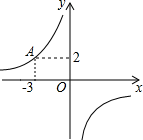 (1)、求这个反比例函数的解析式;(2)、若B(x1 , y1),C(x2 , y2),D(x3 , y3)是这个反比例函数图象上的三个点,若x1>x2>0>x3 , 请比较y1 , y2 , y3的大小,并说明理由.23. 如图,两根竹竿 和 斜靠在墙 上,量得 , , ,求竹竿 和 的长(结果精确到 ).(参考数据: , , , ).
(1)、求这个反比例函数的解析式;(2)、若B(x1 , y1),C(x2 , y2),D(x3 , y3)是这个反比例函数图象上的三个点,若x1>x2>0>x3 , 请比较y1 , y2 , y3的大小,并说明理由.23. 如图,两根竹竿 和 斜靠在墙 上,量得 , , ,求竹竿 和 的长(结果精确到 ).(参考数据: , , , ). 24. 某景区在同一线路上顺次有三个景点A,B,C,甲、乙两名游客从景点A出发,甲步行到景点C;乙花20分钟时间排队后乘观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离景点A的路程s(米)关于时间t(分钟)的函数图象如图所示.
24. 某景区在同一线路上顺次有三个景点A,B,C,甲、乙两名游客从景点A出发,甲步行到景点C;乙花20分钟时间排队后乘观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离景点A的路程s(米)关于时间t(分钟)的函数图象如图所示. (1)、甲的速度是米/分钟;(2)、当20≤t≤30时,求乙离景点A的路程s与t的函数表达式;(3)、乙出发后多长时间与甲在途中相遇?(4)、若当甲到达景点C时,乙与景点C的路程为360米,则乙从景点B步行到景点C的速度是多少?25. 如图1,已知AB是⊙O的直径,AC是⊙O的弦,过O点作OF⊥AB交⊙O于点D,交AC于点E,交BC的延长线于点F,点G是EF的中点,连接CG
(1)、甲的速度是米/分钟;(2)、当20≤t≤30时,求乙离景点A的路程s与t的函数表达式;(3)、乙出发后多长时间与甲在途中相遇?(4)、若当甲到达景点C时,乙与景点C的路程为360米,则乙从景点B步行到景点C的速度是多少?25. 如图1,已知AB是⊙O的直径,AC是⊙O的弦,过O点作OF⊥AB交⊙O于点D,交AC于点E,交BC的延长线于点F,点G是EF的中点,连接CG (1)、判断CG与⊙O的位置关系,并说明理由;(2)、求证:2OB2=BC•BF;(3)、如图2,当∠DCE=2∠F,CE=3,DG=2.5时,求DE的长.26. 如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA交于点E , 连接AC、BD交于点F , 作AH⊥CE , 垂足为点H , 已知∠ADE=∠ACB .
(1)、判断CG与⊙O的位置关系,并说明理由;(2)、求证:2OB2=BC•BF;(3)、如图2,当∠DCE=2∠F,CE=3,DG=2.5时,求DE的长.26. 如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA交于点E , 连接AC、BD交于点F , 作AH⊥CE , 垂足为点H , 已知∠ADE=∠ACB .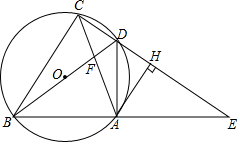 (1)、求证:AH是⊙O的切线;(2)、若OB=4,AC=6,求sin∠ACB的值;(3)、若 ,求证:CD=DH .
(1)、求证:AH是⊙O的切线;(2)、若OB=4,AC=6,求sin∠ACB的值;(3)、若 ,求证:CD=DH .