浙江省宁波市北仑区2019届数学中考模拟试卷

试卷更新日期：2019-09-03 类型：中考模拟

进入 出卷网 下载

一、单选题

  • 1. 2的相反数是（ ）
    A、   12 B、- 12 C、± 12 D、﹣2

    查看试题解析

  • 2. 下列运算，其中正确的是（   ）
    A、2a﹣a＝2 B、（a2）3＝a5 C、a•a3＝a4 D、（a+b）2＝a2+b2

    查看试题解析

  • 3. 如图，四个图标分别是北京大学、人民大学、浙江大学和宁波大学的校徽的重要组成部分，其中是轴对称图形的有（   ）

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 4. 继2017年北仓区经济总量迈上1000亿元的新台阶，2018年再创新高，全年生产总值约1147亿元，1147亿用科学记数法表示为（   ）
    A、1.147×108 B、1.147×109 C、1.147×1010 D、1.147×1011

    查看试题解析

  • 5. 某校7个班同学积极捐出自己的零花钱献爱心，各班捐款的数额分别是（单位：元）：500，200，500，300，500，250，1350．这组数据的众数和中位数分别是（     ）

    A、500，200 B、500，500 C、500，300 D、1350，500

    查看试题解析

  • 6. 如图，由五个小正方体组成的几何体中，若每个小正方体的棱长都是1，则该几何体的左视图和俯视图的面积之和为（   ）

    A、6 B、7 C、8 D、9

    查看试题解析

  • 7. 若实数a＜0，则下列事件中是必然事件的是（   ）
    A、a3＞0 B、3a＞0 C、a+3＜0 D、a﹣3＜0

    查看试题解析

  • 8. 一个圆锥高为4，母线长为5，则这个圆锥的侧面积为（   ）
    A、15π B、12π C、25π D、20π

    查看试题解析

  • 9. 将一副三角板如图放置，使点A在DE上，BC∥DE，则∠ACE的度数为（   ）

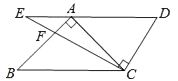    A、10° B、15° C、20° D、25°

    查看试题解析

  • 10. 将抛物线y＝x2沿直线y＝x向上平移 2 个单位，得到的抛物线的解析式为（   ）
    A、y＝（x+1）2+1 B、y＝（x+1）2﹣1 C、y＝（x﹣1）2+1 D、y＝（x﹣1）2﹣1

    查看试题解析

  • 11. 如图，半径为1的⊙O与正五边形ABCDE相切于点A，C，则劣弧AC的长度为（   ）

    A、25π B、23π C、34π D、45π

    查看试题解析

  • 12. 如图，将曲线c1：y＝ kx （x＞0）绕原点O逆时针旋转60°得到曲线c2 ， A为直线y＝ 3 x上一点，P为曲线c2上一点，PA＝PO，且△PAO的面积为6 3 ，直线y＝ 3 x交曲线c1于点B，则OB的长（   ）

    A、2 6 B、5 C、3 3 D、523

    查看试题解析

二、填空题

  • 13. 写出一个小于4的无理数.

    查看试题解析

  • 14. 使代数式 x+1x−2 有意义的x的取值范围是 ．

    查看试题解析

  • 15. 一个布袋里放有红色、黄色、黑色三种球，它们除颜色外其余都相同.红色、黄色、黑色的个数之比为4:3:2,则从布袋里任意摸出1个球不是红球的概率是 ．

    查看试题解析

  • 16. 将多项式ax2﹣4ax+4a分解因式为.

    查看试题解析

  • 17. 如图，在矩形纸片ABCD中，BM，DN分别平分∠ABC，∠CDA，沿BP折叠，点A恰好落在BM上的点E处，延长PE交DN于点F沿DQ折叠，点C恰好落在DN上的点G处，延长QG交BM于点H，若四边形EFGH恰好是正方形，且边长为1，则矩形ABCD的面积为.

    查看试题解析

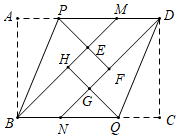  • 18. 如图，菱形ABCD的边长为4，∠A＝60°，E是边AD的中点，F是边BC上的一个动点，EG＝EF，且∠GEF＝60°，则GB+GC的最小值为.

    查看试题解析

三、解答题

  • 19. 先化简，再求值：x（x﹣2）﹣（x+3）（x﹣3），其中 x=(12)−2 .

    查看试题解析

  • 20. 为了解学生参加户外活动的情况，某市教育行政部门对部分学生参加户外活动的时间进行了抽样调查，并将调查结果绘制成下列两幅不完整的统计图，请你根据图中提供的信息解答以下问题：

    (1)、这次抽样共调查了多少名学生？，并补全条形统计图；
    (2)、计算扇形统计图中表示户外活动时间0.5小时的扇形圆心角度数；
    (3)、求出本次调查学生参加户外活动的平均时间.

    查看试题解析

  • 21. 只用直尺（无刻度）完成下列作图：

    (1)、如图1，过正方形ABCD的顶点A作一条直线平分这个正方形的面积；
    (2)、如图2，不过正方形EFGH的顶点作直线l平分这个正方形的面积；
    (3)、如图3，五个边长相等的正方形组成了一个“L型”图形，作直线m平分这个“L型”图形的面积.

    查看试题解析

  • 22. 某爱心企业在政府的支持下投入资金，准备修建一批室外简易的足球场和篮球场，供市民免费使用，修建1个足球场和1个篮球场共需8.5万元，修建2个足球场和4个篮球场共需27万元．
    (1)、求修建一个足球场和一个篮球场各需多少万元？
    (2)、该企业预计修建这样的足球场和篮球场共20个，投入资金不超过90万元，求至少可以修建多少个足球场？

    查看试题解析

  • 23. 如图1，是小明荡秋千的侧面示意图，秋千链长AB＝5m（秋千踏板视作一个点），静止时秋千位于铅垂线BC上，此时秋千踏板A到地面的距离为0.5m.

    (1)、当摆角为37°时，求秋千踏板A与地面的距离AH；（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）
    (2)、如图2，当秋千踏板摆动到点D时，点D到BC的距离DE＝4m；当他从D处摆动到D'处时，恰好D'B⊥DB，求点D'到BC的距离.

    查看试题解析

  • 24. 如图，在平面直角坐标系中，直线 y=−12x+2 分别交x轴，y轴于点A，B抛物线 y=ax2−32x−2 经过点A，且交x轴于另外一点C，交y轴于点D.

    (1)、求抛物线的表达式；
    (2)、求证：AB⊥BC；
    (3)、点P为x轴上一点，过点P作x轴的垂线交直线AB于点M，交抛物线于点Q，连结DQ，设点P的横坐标为m，当以B，D，Q，M为顶点的四边形是平行四边形时，求m的值.

    查看试题解析

  • 25. 如果一个三角形有一条边上的高等于这条边的一半，那么我们把这个三角形叫做“半高三角形”.

    如图1，对于△ABC，BC边上的高AD等于BC的一半，△ABC就是半高三角形，此时，称△ABC是BC类半高三角形；如图2，对于△EFG，EF边上的高GH等于EF的一半，△EFG就是半高三角形，此时，称△EFG是EF类半高三角形.

    (1)、直接写出下列3个小题的答案.

    ①若一个三角形既是等腰三角形又是半高三角形，则其底角度数的所有可能值为.

    ②若一个三角形既是直角三角形又是半高三角形，则其最小角的正切值为.

    ③如图3，正方形网格中，L，M是已知的两个格点，若格点N使得△LMN为半高三角形，且△LMN为等腰三角形或直角三角形，则这样的格点N共有个.

    (2)、如图，平面直角坐标系内，直线y＝x+2与抛物线y＝x2交于R，S两点，点T坐标为（0，5），点P是抛物线y＝x2上的一个动点，点Q是坐标系内一点，且使得△RSQ为RS类半高三角形.

    ①当点P介于点R与点S之间（包括点R，S），且PQ取得最小值时，求点P的坐标.

    ②当点P介于点R与点O之间（包括点R，O）时，求PQ+ 22 QT的最小值.

    查看试题解析

  • 26. 如图1，在平面直角坐标系内，A，B为x轴上两点，以AB为直径的⊙M交y轴于C，D两点，C为 AE⌢ 的中点，弦AE交y轴于点F，且点A的坐标为（2，0），CD＝8

    (1)、求⊙M的半径；
    (2)、动点P在⊙M的圆周上运动.

    ①如图1，当FP的长度最大时，点P记为P，在图1中画出点P0 ， 并求出点P0横坐标a的值；

    ②如图1，当EP平分∠AEB时，求EP的长度；

    ③如图2，过点D作⊙M的切线交x轴于点Q，当点P与点A，B不重合时，请证明 OPPQ 为定值.

    查看试题解析