浙江省宁波市2019届数学中考最后一卷
试卷更新日期:2019-09-03 类型:中考模拟
一、单选题
-
1. 下列实数中,最大的数是( )A、﹣|﹣4| B、0 C、1 D、﹣(﹣3)2. 2018年国庆小长假,泰安市旅游再次交出漂亮“成绩单”,全市纳入重点监测的21个旅游景区、旅游大项目、乡村旅游点实现旅游收入近132000000元,将132000000用科学记数法表示为( )A、 1.32×109 B、1.32×108 C、1.32×107 D、1.32×1063. 下列设计的图案中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、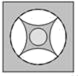 C、
C、 D、
D、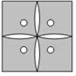 4. 下列运算正确的是( )A、a3•a4=a12 B、a5÷a﹣3=a2 C、(3a4)2=6a8 D、(﹣a)5•a=﹣a65. 有一组数据:2,5,7,2,3,3,6,下列结论错误的是( )A、平均数为4 B、中位数为3 C、众数为2 D、极差是56. 如图是空心圆柱,则空心圆柱在正面的视图,正确的是( )
4. 下列运算正确的是( )A、a3•a4=a12 B、a5÷a﹣3=a2 C、(3a4)2=6a8 D、(﹣a)5•a=﹣a65. 有一组数据:2,5,7,2,3,3,6,下列结论错误的是( )A、平均数为4 B、中位数为3 C、众数为2 D、极差是56. 如图是空心圆柱,则空心圆柱在正面的视图,正确的是( )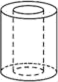 A、
A、 B、
B、 C、
C、 D、
D、 7. 在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是( )
7. 在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是( )
A、2 B、3 C、 D、8. 已知正n边形的一个内角为135°,则边数n的值是( )A、10 B、8 C、7 D、69. 如图,点B、C、D在⊙O上,若∠BCD=140°,则∠BOD的度数是( ) A、40° B、50° C、80° D、90°10. 已知关于x的一元二次方程x2﹣2kx+6=0有两个相等的实数根,则k的值为( )A、±2 B、± C、2或3 D、 或11. 在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
A、40° B、50° C、80° D、90°10. 已知关于x的一元二次方程x2﹣2kx+6=0有两个相等的实数根,则k的值为( )A、±2 B、± C、2或3 D、 或11. 在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( ) A、( ,0) B、(2,0) C、( ,0) D、(3,0)12. 如图,在菱形ABCD中,∠A=60°,AD=4,点F是AB的中点,过点F作FE⊥AD,垂足为E,将△AEF沿点A到点B的方向平移,得到△A'E'F',设点P、P'分别是EF、E'F'的中点,当点A'与点B重合时,四边形PP'CD的面积为( )
A、( ,0) B、(2,0) C、( ,0) D、(3,0)12. 如图,在菱形ABCD中,∠A=60°,AD=4,点F是AB的中点,过点F作FE⊥AD,垂足为E,将△AEF沿点A到点B的方向平移,得到△A'E'F',设点P、P'分别是EF、E'F'的中点,当点A'与点B重合时,四边形PP'CD的面积为( ) A、7 B、6 C、8 D、8 ﹣4
A、7 B、6 C、8 D、8 ﹣4二、填空题
-
13. 把多项式m2﹣4m+4分解因式的结果是.14. 为迎接文明城市的验收工作,某居委会组织两个检查组,分别对“垃圾分类”和“违规停车”的情况进行抽查。各组随机抽取辖区内某三个小区中的一个进行检查,则两个组恰好抽到同一个小区的概率是.15. 不等式组 的解集是 .16. 如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则 的值为.
 17. 如图,坐标平面上,二次函数y=﹣x2+4x﹣k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:3,则k值为.
17. 如图,坐标平面上,二次函数y=﹣x2+4x﹣k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:3,则k值为.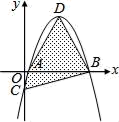 18. 如图,△ABC中,∠ACB=90°,AB=5,AC=3,BC为半圆O的直径,将△ABC沿射线CB方向平移得到△A1B1C1.当A1B1与半圆O相切于点D时,平移的距离的长为.
18. 如图,△ABC中,∠ACB=90°,AB=5,AC=3,BC为半圆O的直径,将△ABC沿射线CB方向平移得到△A1B1C1.当A1B1与半圆O相切于点D时,平移的距离的长为.
三、解答题
-
19. 先化简,再求值: ,其中a= +2.20. 如图,△ABC三个顶点坐标分别为A(﹣1,3),B(﹣1,1),C(﹣3,2).
 (1)、①将△ABC向右平移4个单位,请画出平移后的△A1B1C1;
(1)、①将△ABC向右平移4个单位,请画出平移后的△A1B1C1;②以原点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2 , 请在网格内画出△A2B2C2;
(2)、请在x轴上找出点P,使得点P到B与点A1距离之和最小,请直接写出P点的坐标.21. 随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题: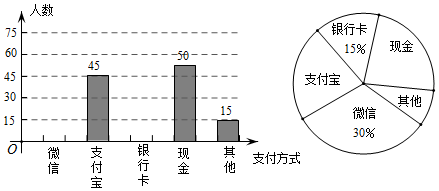 (1)、这次活动共调查了人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为;(2)、将条形统计图补充完整.观察此图,支付方式的“众数”是“”;(3)、在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.22. 如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD.连接MF,NF.
(1)、这次活动共调查了人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为;(2)、将条形统计图补充完整.观察此图,支付方式的“众数”是“”;(3)、在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.22. 如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD.连接MF,NF. (1)、判断△BMN的形状,并证明你的结论;(2)、判断△MFN与△BDC之间的关系,并说明理由.23. 如图,一次函数y=kx+b与反比例函数y= 的图象交于A(2,3),B(﹣3,n)两点.
(1)、判断△BMN的形状,并证明你的结论;(2)、判断△MFN与△BDC之间的关系,并说明理由.23. 如图,一次函数y=kx+b与反比例函数y= 的图象交于A(2,3),B(﹣3,n)两点.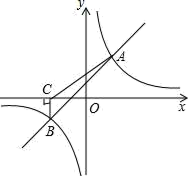 (1)、求一次函数与反比例函数的解析式;(2)、过点B作BC⊥x轴,垂足为C,连接AC,求△ABC的面积.24. 某校为了改善办公条件,计划从厂家购买A、B两种型号电脑.已知每台A种型号电脑价格比每台B种型号电脑价格多0.1万元,且用10万元购买A种型号电脑的数量与用8万购买B种型号电脑的数量相同.(1)、求A、B两种型号电脑每台价格各为多少万元?(2)、学校预计用不多于9.2万元的资金购进这两种电脑共20台,其中A种型号电脑至少要购进10台,请问有哪几种购买方案?25. 如图,在△ABC中,AB=AC=10,以AB为直径的OO与BC相交于点D,与AC相交于点E,DF⊥AC,垂足为F,连接DE,过点A作AG⊥DE,垂足为G,AG与⊙O交于点H.
(1)、求一次函数与反比例函数的解析式;(2)、过点B作BC⊥x轴,垂足为C,连接AC,求△ABC的面积.24. 某校为了改善办公条件,计划从厂家购买A、B两种型号电脑.已知每台A种型号电脑价格比每台B种型号电脑价格多0.1万元,且用10万元购买A种型号电脑的数量与用8万购买B种型号电脑的数量相同.(1)、求A、B两种型号电脑每台价格各为多少万元?(2)、学校预计用不多于9.2万元的资金购进这两种电脑共20台,其中A种型号电脑至少要购进10台,请问有哪几种购买方案?25. 如图,在△ABC中,AB=AC=10,以AB为直径的OO与BC相交于点D,与AC相交于点E,DF⊥AC,垂足为F,连接DE,过点A作AG⊥DE,垂足为G,AG与⊙O交于点H. (1)、求证:DF是⊙O的切线;(2)、若∠CAG=25°,求弧AH的长;(3)、若tan∠CDF= ,求AE的长;26. 如图,直线AB和抛物线的交点是A(0,﹣3),B(5,9),已知抛物线的顶点D的横坐标是2.
(1)、求证:DF是⊙O的切线;(2)、若∠CAG=25°,求弧AH的长;(3)、若tan∠CDF= ,求AE的长;26. 如图,直线AB和抛物线的交点是A(0,﹣3),B(5,9),已知抛物线的顶点D的横坐标是2.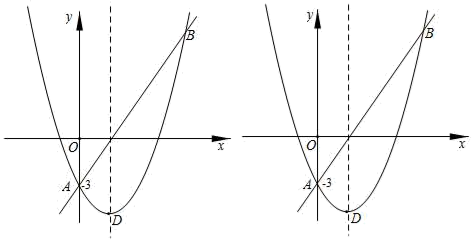 (1)、求抛物线的解析式及顶点坐标;(2)、在x轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不在,请说明理由;(3)、在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
(1)、求抛物线的解析式及顶点坐标;(2)、在x轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不在,请说明理由;(3)、在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.