浙江省宁波市2019届数学中考模拟信息卷

试卷更新日期：2019-09-03 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣ $\frac{2}{3}$ 的相反数是（）

A、﹣ $\frac{2}{3}$ B、 $\frac{3}{2}$ C、 $\frac{2}{3}$ D、﹣ $\frac{3}{2}$

查看试题解析
2. 2018年春节期间共有7.68亿人选择使用微信红包传递新年祝福，收发红包总人数同比去年增加约10%，7.68亿用科学记数法可以表示为（）

A、 7.68×10⁹ B、7.68×10⁸ C、0.768×10⁹ D、0.768×10¹⁰

查看试题解析
3. 下列图形中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列各式计算正确的是（）

A、 ${(- 1)}^{0} - {(\frac{1}{2})}^{- 1} = - 3$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $- 2 \leq x ≺ 3$ D、 ${(a^{2})}^{3} = a^{6}$

查看试题解析
5. 如图，将△ABC绕点C顺时针旋转，点B的对应点为点E，点A的对应点为点D，当点E恰好落在边AC上时，连接AD，若∠ACB=30°，则∠DAC的度数是（）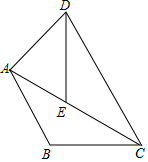

A、 $60^{\circ}$ B、 $65^{\circ}$ C、 $70^{\circ}$ D、 $75^{\circ}$

查看试题解析
6. 关于x的一元二次方程（m﹣1）x²+3x+m²﹣1=0的一根为0，则m的值是（）

A、±1 B、±2 C、﹣1 D、﹣2

查看试题解析
7. 有一张矩形纸片ABCD，AB=2.5，AD=1.5，将纸片折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F（如图），则CF的长为（）

A、1 $\frac{1}{3}$ B、1 C、 $\frac{2}{3}$ D、 $\frac{1}{2}$

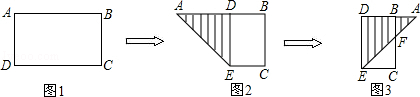查看试题解析
8. 如图，ABCDEF为⊙O的内接正六边形，AB＝m，则图中阴影部分的面积是（）

A、 $\frac{π}{6}$ m² B、 $\frac{\sqrt{3}}{4}$ m² C、 $(\frac{π}{3} - \frac{\sqrt{3}}{4})$ m² D、 $(\frac{π}{6} - \frac{\sqrt{3}}{4})$ m²

查看试题解析
9. 在同一直角坐标系中，函数y＝ $\frac{k}{x}$ 和y＝kx﹣2的图象大致是（）

A、 B、 C、 D、

查看试题解析
10. 如图，三角形ABC沿着BC方向平移得到三角形A′B′C′，P是直线AA′上任意一点，若三角形ABC，三角形PB′C′的面积分别为S₁ ， S₂ ，则下列关系正确的是（）

A、S₁＞S₂ B、S₁＜S₂ C、S₁＝S₂ D、S₁＝2S₂

查看试题解析
11. 如图①，在正方形ABCD中，点P沿边DA从点D开始向点A以1cm/s的速度移动：同时点Q沿边AB，BC从点A开始向点C以acm/s的速度移动，当点P移动到点A时，P，Q同时停止移动.设点P出发x秒时，△PAQ的面积为ycm² ， y与x的函数图象如图②，线段EF所在的直线对应的函数关系式为y＝﹣4x+21，则a的值为（）

A、1.5 B、2 C、3 D、4

查看试题解析
12. 如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为边向外作正方形ACDE，BCFG，DE，FG， $\hat{AC} ， \hat{BC}$ 的中点分别是M，N，P，Q.若MP+NQ＝14，AC+BC＝20，则AB的长是（）

A、9 $\sqrt{2}$ B、 $\frac{90}{7}$ C、13 D、16

查看试题解析

二、填空题

13. 4x²﹣36因式分解的结果.

查看试题解析
14. 若分式方程 $\frac{x}{x - 4} = 2 + \frac{a}{x - 4}$ 的解为正数，则a的取值范围是．

查看试题解析
15. 在不透明的盒子中装有5个黑色棋子和若干个白色棋子，每个棋子除颜色外都相同.任意摸出1个棋子，摸到黑色棋子的概率是 $\frac{1}{4}$ ，则白色棋子的个数是.

查看试题解析
16.
如图，∠AOB是放置在正方形网格中的一个角，则cos∠AOB的值是．

查看试题解析
17. 如图，平面直角坐标系中，OB在x轴上，∠ABO＝90°，点A的坐标为（1，2）.将△AOB绕点A逆时针旋转90°，点O的对应点C恰好落在双曲线y＝ $\frac{k}{x}$ 的一个分支上，过C点的直线y＝﹣x+b与双曲线的另一个交点为E，则△EOC的面积为.

查看试题解析
18. 李老师从“淋浴龙头”受到启发，编了一个题目：在数轴上截取从0到3的对应线段AB，实数m对应AB上的点M，如图1；将AB折成正三角形，使点A，B重合于点P，如图2；建立平面直角坐标系，平移此三角形，使它关于y轴对称，且点P的坐标为（0，2），PM与x轴交于点N（n，0），如图3.当m＝ $\sqrt{3}$ 时，n＝.

查看试题解析

三、解答题

19. 先化简，再求值： $\frac{x^{2} - 2 x}{x^{2} - 1} \div (x - 1 - \frac{2 x - 1}{x + 1})$ ，其中x是满足|x|≤2的整数.

查看试题解析
20. 如图，在平面直角坐标系中，已知△AOB，A（0，﹣3），B（﹣2，0）.将△OAB先绕点B逆时针旋转90°得到△BO₁A₁ ，再把所得三角形向上平移2个单位得到△B₁A₂O₂；

(1)、在图中画出上述变换的图形，并涂黑；

(2)、求△OAB在上述变换过程所扫过的面积.

查看试题解析
21. 某校九年级开展征文活动，征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个，九年级每名学生按要求都上交了一份征文，学校为了解选择各种征文主题的学生人数，随机抽取了部分征文进行了调查，根据调查结果绘制成如下两幅不完整的统计图．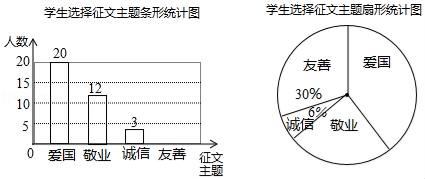

(1)、求共抽取了多少名学生的征文；

(2)、将上面的条形统计图补充完整；

(3)、在扇形统计图中，选择“爱国”主题所对应的圆心角是多少；

(4)、如果该校九年级共有1200名学生，请估计选择以“友善”为主题的九年级学生有多少名．

查看试题解析
22. 如图.在平行四边形ABCD中，过点B作BM⊥AC于点E，交CD于点M，过点D作DN⊥AC于点F，交AB于点N.

(1)、求证：四边形BMDN是平行四边形；

(2)、已知AF＝5，EM＝3，求AN的长.

查看试题解析
23. 如图，在平面直角坐标系中，过点A $(1 ， \frac{20}{3}) B (4 ， \frac{8}{3})$ 的直线l分别与x轴、y轴交于点C，D.

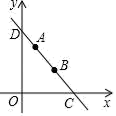(1)、求直线l的函数表达式.

(2)、P为x轴上一点，若△PCD为等腰三角形直接写出点P的坐标.

(3)、将线段AB绕B点旋转90°，直接写出点A对应的点A的坐标.

查看试题解析
24. 某青春党支部在精准扶贫活动中，给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种．已知乙种树苗的价格比甲种树苗贵10元，用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同．

(1)、求甲、乙两种树苗每棵的价格各是多少元？

(2)、在实际帮扶中，他们决定再次购买甲、乙两种树苗共50棵，此时，甲种树苗的售价比第一次购买时降低了10%，乙种树苗的售价不变，如果再次购买两种树苗的总费用不超过1500元，那么他们最多可购买多少棵乙种树苗？

查看试题解析
25. 如图，已知：AB是⊙O的直径，点C在⊙O上，CD是⊙O的切线，AD⊥CD于点D，E是AB延长线上一点，CE交⊙O于点F，连接OC、AC.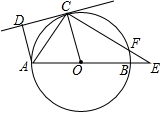

(1)、求证：AC平分∠DAO.

(2)、若∠DAO=105°，∠E=30°
①求∠OCE的度数；

②若⊙O的半径为2 $\sqrt{2}$ ，求线段EF的长.

查看试题解析
26. 如图，在平面直角坐标中，抛物线y＝ax²+bx+c过点A（﹣1，0），B（3，0），C（0，3），点P是直线BC上方抛物线上的一动点，PE∥y轴，交直线BC于点E连接AP，交直线BC于点D.

(1)、求抛物线的函数表达式；

(2)、当AD＝2PD时，求点P的坐标；

(3)、求线段PE的最大值；

(4)、当线段PE最大时，若点F在直线BC上且∠EFP＝2∠ACO，直接写出点F的坐标.

查看试题解析