浙江省丽水市莲都区2019届数学中考模拟试卷(6月)
试卷更新日期:2019-09-03 类型:中考模拟
一、单选题
-
1. -2的相反数的倒数是( )A、2 B、 C、 D、2. 计算:(﹣a2)3=( )A、a6 B、﹣a6 C、a5 D、﹣a53. 下列立体图形中,主视图是三角形的是( )A、
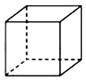 B、
B、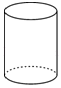 C、
C、 D、
D、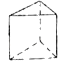 4. 分式 可变形为( )A、 B、 C、 D、5. 如图,要测量小河两岸相对的A,B两点之间的距离,可以在小河边取AB的垂线BC上的一点D,若测得BD=60米,∠ADB=40°,则AB等于( )
4. 分式 可变形为( )A、 B、 C、 D、5. 如图,要测量小河两岸相对的A,B两点之间的距离,可以在小河边取AB的垂线BC上的一点D,若测得BD=60米,∠ADB=40°,则AB等于( ) A、60tan40°米 B、60tan50°米 C、60sin40°米 D、60sin50°米6. 在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号是奇数的概率为( )A、 B、 C、 D、7. 三角形的两边长分别为3和4,第三边长是方程x2﹣13x+40=0的根,则该三角形的周长是( )A、12 B、13 C、15 D、12或158. 在平面直角坐标系中,将点A(﹣1,1)向右平移2个单位长度得到点B,则点B关于x轴的对称点B的坐标为( )A、(﹣3,﹣1) B、(1,﹣1) C、(﹣1,1) D、(﹣1,﹣3)9. 如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于 AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )
A、60tan40°米 B、60tan50°米 C、60sin40°米 D、60sin50°米6. 在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号是奇数的概率为( )A、 B、 C、 D、7. 三角形的两边长分别为3和4,第三边长是方程x2﹣13x+40=0的根,则该三角形的周长是( )A、12 B、13 C、15 D、12或158. 在平面直角坐标系中,将点A(﹣1,1)向右平移2个单位长度得到点B,则点B关于x轴的对称点B的坐标为( )A、(﹣3,﹣1) B、(1,﹣1) C、(﹣1,1) D、(﹣1,﹣3)9. 如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于 AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )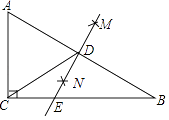 A、AD=BD B、BD=CD C、∠A=∠BED D、∠ECD=∠EDC10. 甲、乙二人从学校出发去新华书店看书,甲步行一段时间后,乙骑自行车沿相同路线行进两人均匀速前行,他们之间的距离s(米)与甲出发时间t(分)之间的函数关系如图所示.下列说法错误的是( )
A、AD=BD B、BD=CD C、∠A=∠BED D、∠ECD=∠EDC10. 甲、乙二人从学校出发去新华书店看书,甲步行一段时间后,乙骑自行车沿相同路线行进两人均匀速前行,他们之间的距离s(米)与甲出发时间t(分)之间的函数关系如图所示.下列说法错误的是( )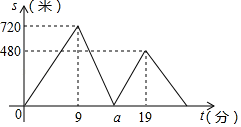 A、乙的速度是甲速度的2.5倍 B、a=15 C、学校到新华书店共3800米 D、甲第25分钟到达新华书店
A、乙的速度是甲速度的2.5倍 B、a=15 C、学校到新华书店共3800米 D、甲第25分钟到达新华书店二、填空题
-
11. 分解因式:2m2﹣2= .12. 若a﹣2b=﹣3,则代数式1﹣a+2b的值为.13. 某校901班共有50名同学,如图是该次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数),则测试成绩的中位数所在的组别是.
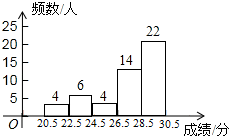 14. 如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AEC=40°,则∠BDC的度数为.
14. 如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AEC=40°,则∠BDC的度数为.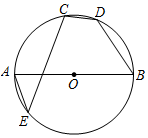 15. 如图①,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成.若直角三角形一个锐角为30°,将各三角形较短的直角边分别向外延长一倍,得到图②所示的“数学风车”设AB=a,则图中阴影部分面积为(用含a的代数式表示)
15. 如图①,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成.若直角三角形一个锐角为30°,将各三角形较短的直角边分别向外延长一倍,得到图②所示的“数学风车”设AB=a,则图中阴影部分面积为(用含a的代数式表示) 16. 如图,矩形纸片ABCD中,AB=4,点E在边CD上移动连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′CE,点B、C的对应点分别为点B′、C′
16. 如图,矩形纸片ABCD中,AB=4,点E在边CD上移动连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′CE,点B、C的对应点分别为点B′、C′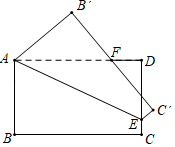 (1)、当点E与点C重合时,设B′C′与AD的交点为F,若AD=4DF,则AD=(2)、若AD=6,B′C′的中点记为P,则DP的取值范围是
(1)、当点E与点C重合时,设B′C′与AD的交点为F,若AD=4DF,则AD=(2)、若AD=6,B′C′的中点记为P,则DP的取值范围是三、解答题
-
17. 计算: .18. 解方程组:19. 图是5×5的网格图,每个小正方形的边长为1,请按要求作格点图形(图形的每个顶点都在格点上)
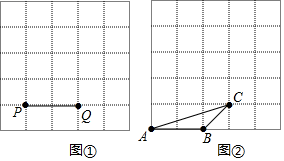 (1)、在图①中以线段PQ为一边作一个等腰直角三角形;(2)、在图②中,作△DEF相似于△ABC,且△ABC与△DEF的相似比是1: .20. 为做好全国文明城市的创建工作,我市交警连续10天对某路口100个“50岁以下行人”和100个“50岁及以上行人”中出现交通违章的情况进行了调查统计,将所得数据绘制成如下统计图.请根据所给信息,解答下列问题
(1)、在图①中以线段PQ为一边作一个等腰直角三角形;(2)、在图②中,作△DEF相似于△ABC,且△ABC与△DEF的相似比是1: .20. 为做好全国文明城市的创建工作,我市交警连续10天对某路口100个“50岁以下行人”和100个“50岁及以上行人”中出现交通违章的情况进行了调查统计,将所得数据绘制成如下统计图.请根据所给信息,解答下列问题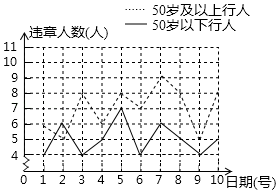 (1)、求这10天“50岁及以上行人”中每天违章人数的众数;(2)、某天中午下班时段经过这一路口的“50岁以下行人”为300人,请估计大约有多少人会出现交通违章行为;(3)、请选择适当的统计量分析“50岁以下行人”和“50岁以上行人”交通违章行为的现并就“文明城市创建减少交通违章”提出合理建议.21. 已知,平面直角坐标系中,关于x的二次函数y=x2﹣2mx+m2﹣2(1)、若此二次函数的图象过点A(﹣1,﹣2),求函数的表达式;(2)、若(x1 , y1),(x2 , y2)为此二次函数图象上两个不同点,且x1+x2=4时y1=y2 , 试求m的值;(3)、点P(﹣2,y3)在抛物线上,求y3的最小值.22. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CAB=2∠CBF
(1)、求这10天“50岁及以上行人”中每天违章人数的众数;(2)、某天中午下班时段经过这一路口的“50岁以下行人”为300人,请估计大约有多少人会出现交通违章行为;(3)、请选择适当的统计量分析“50岁以下行人”和“50岁以上行人”交通违章行为的现并就“文明城市创建减少交通违章”提出合理建议.21. 已知,平面直角坐标系中,关于x的二次函数y=x2﹣2mx+m2﹣2(1)、若此二次函数的图象过点A(﹣1,﹣2),求函数的表达式;(2)、若(x1 , y1),(x2 , y2)为此二次函数图象上两个不同点,且x1+x2=4时y1=y2 , 试求m的值;(3)、点P(﹣2,y3)在抛物线上,求y3的最小值.22. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CAB=2∠CBF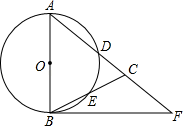 (1)、求证:直线BF是⊙O的切线;(2)、若BC=2 ,sin∠CBF ,求BF的长.23. 平面直角坐标系中,横坐标为2的点A在反比例函数y (k>0)的图象上,过点A作AB⊥x轴于点B, .
(1)、求证:直线BF是⊙O的切线;(2)、若BC=2 ,sin∠CBF ,求BF的长.23. 平面直角坐标系中,横坐标为2的点A在反比例函数y (k>0)的图象上,过点A作AB⊥x轴于点B, . (1)、求k的值;(2)、在x轴的负半轴上找点P,将点A绕点P顺时针旋转90°,其对应点A落在此反比例函数第三象限的图象上,求点P的坐标;(3)、直线y x+n(n<0)与AB的延长线交于点C,与反比例函数图象交于点E,若点E到直线AB的距离等于AC,求n的值.24. 如图,在矩形ABCD中,AB=6,BC=8,点E是BC的中点,点P为对角线BD上的动点,设BP=t(t>0),作PH⊥BC于点H,连接EP并延长至点F,使得PF=PE,作点F关于BD的对称点G,FG交BD于点Q,连接GH,GE.
(1)、求k的值;(2)、在x轴的负半轴上找点P,将点A绕点P顺时针旋转90°,其对应点A落在此反比例函数第三象限的图象上,求点P的坐标;(3)、直线y x+n(n<0)与AB的延长线交于点C,与反比例函数图象交于点E,若点E到直线AB的距离等于AC,求n的值.24. 如图,在矩形ABCD中,AB=6,BC=8,点E是BC的中点,点P为对角线BD上的动点,设BP=t(t>0),作PH⊥BC于点H,连接EP并延长至点F,使得PF=PE,作点F关于BD的对称点G,FG交BD于点Q,连接GH,GE. (1)、求证:EG∥PQ;(2)、当点P运动到对角线BD中点时,求△EFG的周长;(3)、在点P的运动过程中,△GEH是否可以为等腰三角形?若可以,求出t的值;若不可以,说明理由.
(1)、求证:EG∥PQ;(2)、当点P运动到对角线BD中点时,求△EFG的周长;(3)、在点P的运动过程中,△GEH是否可以为等腰三角形?若可以,求出t的值;若不可以,说明理由.