浙江省金华市永康市2019届数学中考二模试卷
试卷更新日期:2019-09-03 类型:中考模拟
一、单选题
-
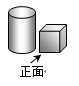
1. 在﹣2,3,0,﹣1中,最小的数是( )A、﹣2 B、3 C、0 D、﹣12. 2018年浙江省生产总值约为56200亿元.数56200用科学记数法表示为( )A、 56.2×103 B、5.62×104 C、562×102 D、0.562×1033. 小明从正面观察下图所示的两个物体,看到的是( )
 A、
A、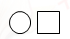 B、
B、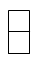 C、
C、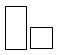 D、
D、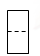 4. 五名男生的体重(单位:kg)分别为50,55,60,55,57,则这组数据的中位数是( )A、50 B、55 C、57 D、605. 如图,直线a∥b,直线c分别与a,b相交,∠1=120°,则∠2的度数为( )
4. 五名男生的体重(单位:kg)分别为50,55,60,55,57,则这组数据的中位数是( )A、50 B、55 C、57 D、605. 如图,直线a∥b,直线c分别与a,b相交,∠1=120°,则∠2的度数为( )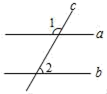 A、60° B、120° C、50° D、70°6. 若代数式 和 的值相等,则x的值为( )A、x=﹣7 B、x=7 C、x=﹣5 D、x=37. 已知点(﹣2,y1),(﹣3,y2),(2,y3)在函数y=﹣ 的图象上,则( )A、y2>y1>y3 B、y1>y2>y3 C、y3>y1>y2 D、y1>y3>y28. 王爷爷上午8:00从家出发,外出散步,到老年阅览室看了一会儿报纸,继续以相同的速度散步一段时间,然后回家.如图描述了王爷爷在散步过程中离家的路程s(米)与所用时间t(分)之间的函数关系,则下列信息错误的是( )
A、60° B、120° C、50° D、70°6. 若代数式 和 的值相等,则x的值为( )A、x=﹣7 B、x=7 C、x=﹣5 D、x=37. 已知点(﹣2,y1),(﹣3,y2),(2,y3)在函数y=﹣ 的图象上,则( )A、y2>y1>y3 B、y1>y2>y3 C、y3>y1>y2 D、y1>y3>y28. 王爷爷上午8:00从家出发,外出散步,到老年阅览室看了一会儿报纸,继续以相同的速度散步一段时间,然后回家.如图描述了王爷爷在散步过程中离家的路程s(米)与所用时间t(分)之间的函数关系,则下列信息错误的是( ) A、王爷爷看报纸用了20分钟 B、王爷爷一共走了1600米 C、王爷爷回家的速度是80米/分 D、上午8:32王爷爷在离家800米处9. 甲,乙两位同学用尺规作“过直线l外一点C作直线l的垂线”时,第一步两位同学都以C为圆心,适当长度为半径画弧,交直线l于D,E两点(如图);第二步甲同学作∠DCE的平分线所在的直线,乙同学作DE的中垂线.则下列说法正确的是( )
A、王爷爷看报纸用了20分钟 B、王爷爷一共走了1600米 C、王爷爷回家的速度是80米/分 D、上午8:32王爷爷在离家800米处9. 甲,乙两位同学用尺规作“过直线l外一点C作直线l的垂线”时,第一步两位同学都以C为圆心,适当长度为半径画弧,交直线l于D,E两点(如图);第二步甲同学作∠DCE的平分线所在的直线,乙同学作DE的中垂线.则下列说法正确的是( ) A、只有甲的画法正确 B、只有乙的画法正确 C、甲,乙的画法都正确 D、甲,乙的画法都不正确10. 已知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示,下列说法中①abc<0;②2a+b=0;③当﹣1<x<3时,y>0;④2c﹣3b<0.正确的结论有( )
A、只有甲的画法正确 B、只有乙的画法正确 C、甲,乙的画法都正确 D、甲,乙的画法都不正确10. 已知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示,下列说法中①abc<0;②2a+b=0;③当﹣1<x<3时,y>0;④2c﹣3b<0.正确的结论有( )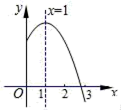 A、①② B、②③④ C、①③ D、①②④
A、①② B、②③④ C、①③ D、①②④二、填空题
-
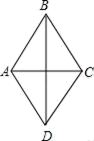
11. 因式分解:3ab+6a=.12. 已知x=3是一元二次方程2ax2﹣ax=5的一个解,则a=.13. 如图,在菱形ABCD中,对角线AC=6,BD=8,则这个菱形的边长为.
 14. 将函数y=2x+1的图象向左平移2个单位所得图象的函数解析式为.15. 在Rt△ABC纸片上剪出7个如图所示的正方形,点E,F落在AB边上,每个正方形的边长为1,则Rt△ABC的面积为.
14. 将函数y=2x+1的图象向左平移2个单位所得图象的函数解析式为.15. 在Rt△ABC纸片上剪出7个如图所示的正方形,点E,F落在AB边上,每个正方形的边长为1,则Rt△ABC的面积为. 16. 我们常见的汽车玻璃升降器如图①所示,图②和图③是升降器的示意图,其原理可以看作是主臂PB绕固定的点O旋转,当端点P在固定的扇形齿轮 上运动时,通过叉臂式结构(点B可在MN上滑动)的玻璃支架MN带动玻璃沿导轨作上下运动而达到玻璃升降目的.点O和点P,A,B在同一直线上.当点P与点E重合时,窗户完全闭合(图②),此时∠ABC=30°;当点P与点F重合时,窗户完全打开(图③).已知 的半径OP=5cm, = cm,OA=AB=AC=20cm.
16. 我们常见的汽车玻璃升降器如图①所示,图②和图③是升降器的示意图,其原理可以看作是主臂PB绕固定的点O旋转,当端点P在固定的扇形齿轮 上运动时,通过叉臂式结构(点B可在MN上滑动)的玻璃支架MN带动玻璃沿导轨作上下运动而达到玻璃升降目的.点O和点P,A,B在同一直线上.当点P与点E重合时,窗户完全闭合(图②),此时∠ABC=30°;当点P与点F重合时,窗户完全打开(图③).已知 的半径OP=5cm, = cm,OA=AB=AC=20cm.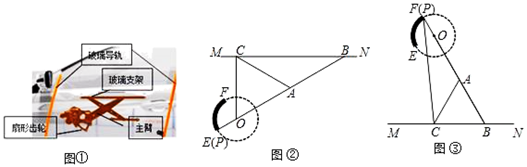 (1)、当窗户完全闭合时,OC=cm.(2)、当窗户完全打开时,PC=cm.
(1)、当窗户完全闭合时,OC=cm.(2)、当窗户完全打开时,PC=cm.三、解答题
-
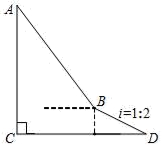
17. 计算: .18. 解不等式组:19. 如图,为了测量建筑物AC的高度,从距离建筑物底部C处50米的点D(点D与建筑物底部C在同一水平面上)出发,沿坡度i=1:2的斜坡DB前进10 米到达点B,在点B处测得建筑物顶部A的仰角为53°,求建筑物AC的高度.(结果精确到0.1米.参考数据:sin53°≈0.798,cos53°≈0.602,tan53°≈1.327.)
 20. 永康市某校在课改中,开设的选修课有:篮球,足球,排球,羽毛球,乒乓球,学生可根据自己的爱好选修一门,李老师对九(1)班全班同学的选课情况进行调查统计,制成了两幅不完整的统计图(如图).
20. 永康市某校在课改中,开设的选修课有:篮球,足球,排球,羽毛球,乒乓球,学生可根据自己的爱好选修一门,李老师对九(1)班全班同学的选课情况进行调查统计,制成了两幅不完整的统计图(如图).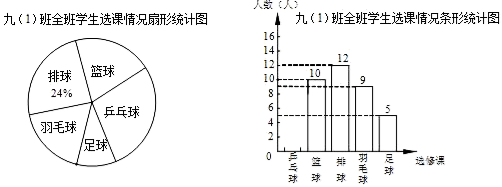 (1)、该班共有学生多少人?并补全条形统计图;(2)、求“篮球”所在扇形圆心角的度数;(3)、九(1)班班委4人中,甲选修篮球,乙和丙选修足球,丁选修排球,从这4人中任选2人,请你用列表或画树状图的方法,求选出的2人中恰好为1人选修篮球,1人选修足球的概率.21. 如图,点O是Rt△ABC斜边AB上的一点,⊙O经过点A与BC相切于点D,分别交AB,AC于E,F,OA=2cm,AC=3cm.
(1)、该班共有学生多少人?并补全条形统计图;(2)、求“篮球”所在扇形圆心角的度数;(3)、九(1)班班委4人中,甲选修篮球,乙和丙选修足球,丁选修排球,从这4人中任选2人,请你用列表或画树状图的方法,求选出的2人中恰好为1人选修篮球,1人选修足球的概率.21. 如图,点O是Rt△ABC斜边AB上的一点,⊙O经过点A与BC相切于点D,分别交AB,AC于E,F,OA=2cm,AC=3cm.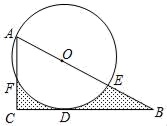 (1)、求BE的长;(2)、求图中阴影部分的面积.22. 如图,已知抛物线y=x2+ax﹣3交x轴于点A,D两点,交y轴于点C,过点A的直线与x轴下方的抛物线交于点B,已知点A的坐标是(﹣1,0).
(1)、求BE的长;(2)、求图中阴影部分的面积.22. 如图,已知抛物线y=x2+ax﹣3交x轴于点A,D两点,交y轴于点C,过点A的直线与x轴下方的抛物线交于点B,已知点A的坐标是(﹣1,0).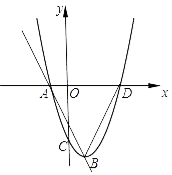 (1)、求a的值;(2)、连结BD,求△ADB面积的最大值;(3)、当△ADB面积最大时,求点C到直线AB的距离.23. 如图
(1)、求a的值;(2)、连结BD,求△ADB面积的最大值;(3)、当△ADB面积最大时,求点C到直线AB的距离.23. 如图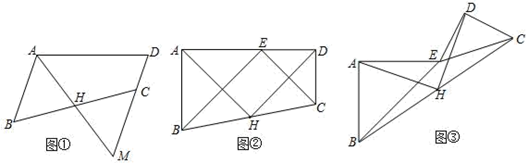 (1)、方法形成
(1)、方法形成如图①,在四边形ABCD中,AB∥DC,点H是BC的中点,连结AH并延长交DC的延长线于M,则有CM=AB.请说明理由;
(2)、方法迁移如图②,在四边形ABCD中,点H是BC的中点,E是AD上的点,且△ABE和△DEC都是等腰直角三角形,∠BAE=∠EDC=90°.请探究AH与DH之间的关系,并说明理由.
(3)、拓展延伸在(2)的条件下,将Rt△DEC绕点E旋转到图③的位置,请判断(2)中的结论是否依然成立?若成立,请说明理由;若不成立,请举例说明.
24. 如图,正方形OABC的顶点O与原点重合,点A,C分别在x轴与y轴的正半轴上,点A的坐标为(4,0),点D在边AB上,且tan∠AOD= ,点E是射线OB上一动点,EF⊥x轴于点F,交射线OD于点G,过点G作GH∥x轴交AE于点H. (1)、求B,D两点的坐标;(2)、当点E在线段OB上运动时,求∠HDA的大小;(3)、以点G为圆心,GH的长为半径画⊙G.是否存在点E使⊙G与正方形OABC的对角线所在的直线相切?若不存在,请说明理由;若存在,请求出所有符合条件的点E的坐标.
(1)、求B,D两点的坐标;(2)、当点E在线段OB上运动时,求∠HDA的大小;(3)、以点G为圆心,GH的长为半径画⊙G.是否存在点E使⊙G与正方形OABC的对角线所在的直线相切?若不存在,请说明理由;若存在,请求出所有符合条件的点E的坐标.