浙江省金华市义乌市2019届数学中考模拟试卷
试卷更新日期：2019-09-03 类型：中考模拟
一、单选题
-
1. 2019的倒数是（ ）A、2019 B、﹣2019 C、 D、﹣2. 如图是由5个相同大小的正方体搭成的几何体，则它的俯视图是（ ）
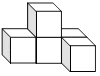A、
B、
C、
D、
3. 下列计算正确的是（ ）A、 ＝3 B、 ＝±3 C、 ＝3 D、 ＝±34. 大课间活动在我市各校蓬勃开展．某班大课间活动抽查了20名学生每分钟跳绳次数，获得如下数据（单位：次）：50，63，77，83，87，88，89，91，93，100，102，111，117，121，130，133，146，158，177，188．则跳绳次数在90～110这一组的频率是（ ）
A、0.1 B、0.2 C、0.3 D、0.75. 如图，AC是平行四边形ABCD的对角线，当它满足以下：①∠1＝∠2；②∠2＝∠3；③∠B＝∠3；④∠1＝∠3中某一条件时，平行四边形ABCD是菱形，这个条件是（ ）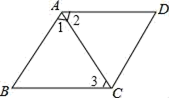
A、①或② B、②或③ C、③或④ D、①或④6. 在平面直角坐标系中，点A（﹣1，5），将点A向右平移2个单位，再向下平移3个单位得到点A1；点A1关于y轴与A2对称，则A2的坐标为（ ）A、（2，﹣1） B、（1，2） C、（﹣1，2） D、（﹣2，1）7. 如图，AB是圆锥的母线，BC为底面半径，已知BC=6cm，圆锥的侧面积为15πcm2 ， 则sin∠ABC的值为（ ）
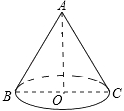A、 B、 C、 D、8. 如图，直线y＝kx+b与y＝mx+n分别交x轴于点A（﹣1，0），B（4，0），则函数y＝（kx+b）（mx+n）中，当y＜0时x的取值范围是（ ）
A、x＞2 B、0＜x＜4 C、﹣1＜x＜4 D、x＜﹣1或x＞49. 如图，在矩形ABCD内放入六个小正方形后形成一个中心对称图形，其中顶点E，F分别在边BC，AD上，则长AD与宽AB的比为（ ）
A、6：5 B、13：10 C、8：7 D、4：310. 某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品，将这些作品排成一个矩形(作品不完全重合).现需要在每张作品的四个角落都钉上图钉，如果作品有角落相邻，那么相邻的角落共享一枚图钉(例如，用9枚图钉将4张作品钉在墙上，如图).若有36枚图钉可供选用，则最多可以展示绘画作品（ ）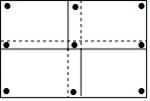
A、22张 B、23张 C、24张 D、25张二、填空题
-
11. 分解因式：3x2﹣27x＝.12. 已知正n边形的每一个内角为150°，则n＝.13. 如图，菱形ABCD的对角线AC，BD相交于点O.若tan∠BAC＝ ，AC＝6，则BD的长是.
14. 如图，点A，B是反比例函数y＝ (x＞0)图象上的两点，过点A，B分别作AC⊥x轴于点C，BD⊥x轴于点D，连接OA，BC，点C(1，0)，BD＝ ，S△BCD＝3，则k＝.
15. 如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝4，D为AB上的动点，以DC为斜边向右侧作等腰Rt△DCE，使∠CED＝90°，连接BE，则线段BE的最小值为.
16. 已知抛物线y＝ax2﹣2ax+c(a＜0)的图象过点A(3，m).
(1)、当a＝﹣1，m＝0时，求抛物线的顶点坐标；(2)、如图，直线l：y＝kx+c(k＜0)交抛物线于B，C两点，点Q(x，y)是抛物线上点B，C之间的一个动点，作QD⊥x轴交直线l于点D，作QE⊥y轴于点E，连接DE.设∠QED＝β，当2≤x≤4时，β恰好满足30°≤β≤60°，a＝.三、解答题
-
17.(1)、计算： ﹣4sin45°+(3﹣π)0+|﹣4|﹣( )﹣2.(2)、解方程： +3＝ .18. 如图，由6个形状、大小完全相同的小矩形组成大矩形网格，小矩形的顶点称为这个矩形网格的格点，由格点构成的四边形称为格点四边形，请按要求作图(标出所画图形的顶点字母).
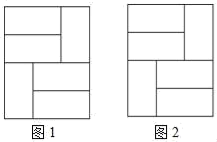
在图1中画出一个格点正方形；
在图2中画出一个一般的格点平行四边形(非菱形、矩形).
19. 宁波轨道交通4号线已开工建设，计划2020年通车试运营.为了了解镇民对4号线地铁票的定价意向，某镇某校数学兴趣小组开展了“你认为宁波4号地铁起步价定为多少合适”的问卷调查，并将调查结果整理后制成了如下统计图，根据图中所给出的信息解答下列问题：
(1)、求本次调查中该兴趣小组随机调查的人数；(2)、请你把条形统计图补充完整；(3)、如果在该镇随机咨询一位居民，那么该居民支持“起步价为2元或3元”的概率是.(4)、假设该镇有3万人，请估计该镇支持“起步价为3元”的居民大约有多少人？20. 某大桥采用低塔斜拉桥桥型（如甲图），图乙是从图甲引申出的平面图，假设你站在桥上测得拉索AB与水平桥面的夹角是30°，拉索CD与水平桥面的夹角是60°，两拉索顶端的距离BC为2米，两拉索底端距离AD为20米，请求出立柱BH的长.（结果精确到0.1米， ≈1.73）
21. 如图，在Rt△ABC中，点O在斜边AB上，以O为圆心，OB为半径作圆，分别与BC，AB相交于点D，E，连结AD.已知∠CAD=∠B.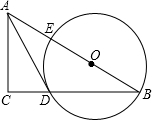
(1)、求证：AD是⊙O的切线.(2)、若BC=8，tanB= ，求⊙O 的半径.22. 儿童游乐场有一项射击游戏，从O处发射小球，将球投入正方形篮筐DABC.正方形篮筐三个顶点为A(2，2)，B(3，2)，D(2，3).小球按照抛物线y＝﹣x2+bx+c飞行.小球落地点P坐标(n，0).
(1)、点C坐标为.(2)、求c，b并写出小球飞行中最高点N的坐标(用含有n的代数式表示)；(3)、若小球发射之后能够直接入篮，球没有接触篮筐，请直接写出n的取值范围.23. 定义：若△ABC中，其中一个内角是另一个内角的一半，则称△ABC为“半角三角形”.
(1)、若Rt△ABC为半角三角形，∠A＝90°，则其余两个角的度数为.(2)、如图1，在▱ABCD中，∠C＝72°，点E在边CD上，以BE为折痕，将△BCE向上翻折，点E恰好落在AD边上的点F，若BF⊥AD，求证：△EDF为半角三角形；(3)、如图2，以△ABC的边AB为直径画圆，与边AC交于M，与边BC交于N，已知△ABC的面积是△CMN面积的4倍.①求证：∠C＝60°.
②若△ABC是半角三角形，直接写出∠B的度数.
24. 如图1，矩形OABC中，OA＝3，OC＝2，以矩形的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系.在直线OA上取一点D，将△BDA沿BD翻折，点A的对应点为点A'，直线DA'与直线BC的交点为F.
(1)、如图2，当点A′恰好落在线段CB上时，取AB的中点E，①直接写出点E、F的坐标；
②设顶点为F的抛物线交y轴正半轴于点P，且以点E、F、P为顶点的三角形是等腰三角形，求该抛物线的解析式；
③在x轴、y轴上是否分别存在点M、N，使得四边形MNFE的周长最小？如果存在，求出周长的最小值；如果不存在，请说明理由.
(2)、在平面内找一点G，连结BG、FG，使四边形A'BGF为正方形，求点D的坐标.