浙江省金华市婺城区2019届数学中考一模试卷
试卷更新日期：2019-09-03 类型：中考模拟
一、单选题
-
1. 下列四个数中，最大的数是（ ）A、π B、3 C、 D、3.142. 2019年3月初，全国“两会”在北京人民大会堂隆重召开，李克强总理在《政府工作报告》中指出，过去的一年，我国为企业和个人减税降费约1300000000000元，数1300000000000用科学记数法表示为（ ）A、 13×108 B、0.13×1013 C、1.3×1012 D、1.3×10133. 下列计算正确的是（ ）A、（﹣a3）2＝a5 B、﹣3a2b+3ba2＝0 C、a2×a3≡a6 D、（﹣3a2b）3＝a6b34. 以下是我市著名企事业（新飞电器、心连心化肥、新乡银行、格美特科技）的徽标或者商标，其中既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
5.如图是由6个相同的小正方体搭成的几何体，那么这个几何体的俯视图是（ ）
A、
B、
C、
D、
6. 若关于x的一元二次方程ax2+bx﹣3＝0（a≠0）的解是x＝﹣1，则﹣5+2a﹣2b的值是（ ）A、0 B、1 C、2 D、37. 已知点（1，y1），（2，y2）（3，y3）均在反比例函数 的图象上，则y1 ， y2 ， y3 ， 的大小关系是（ ）A、y3＜y2＜y1 B、y2＜y3＜y1 C、y1＜y2＜y3 D、y1＜y3＜y28. 若 ，那么yx的值是（ ）A、﹣1 B、 C、1 D、89. 当x＝a和x＝b（a≠b）时，二次函数y＝2x2﹣2x+3的函数值相等、当x＝a+b时，函数y＝2x2﹣2x+3的值是（ ）A、0 B、﹣2 C、1 D、310. 从甲地到乙地，先是一段平路，然后是一段上坡路，小明骑车从甲地出发，到达乙地后立即返回甲地，途中休息了一段时间，假设小明骑车在平路、上坡、下坡时分别保持匀速前进，已知小明骑车上坡的速度比在平路上的速度每小时少5km，下坡的速度比在平路上的速度每小时多5km.设小明出发xh后，到达离甲地ykm的地方，图中的折线OABCDE表示y与x之间的函数关系.①小明骑车在平路上的速度为15km/h②小明途中休息了0.1h；③小明从甲地去乙地来回过程中，两次经过距离甲地5.5km的地方的时间间隔为0.15h则以上说法中正确的个数为（ ）
A、0 B、1 C、2 D、3二、填空题
-
11. 因式分解m3﹣4m＝.12. 试写出一个以 为解的二元一次方程组.13. 如图，若∠A＝15°，AB＝BC＝CD＝DE＝EF，则∠DEF等于.
14. 任意抛掷一枚质地均匀的正方体骰子2次，骰子的6个面上分别刻有1到6的点数，记第一次掷得面朝上的点数为横坐标，第二次掷得面朝上的点数为纵坐标，这样组成的点的坐标恰好在正比例函数y＝x上的概率为.15. 如图，⊙O的直径为 cm，弦AB⊥弦CD于点E，连接AD，BC，若AD＝4cm，则BC的长为cm.
16. 在△ABC中，AB＝ ，BC＝6，∠B＝45°，D为BC边上一点将△ABC沿着过D点的直线折叠，使得点C落在AB边上，记CD＝m，则AC＝ ， m的取值范围是三、解答题
-
17. 计算题： ﹣3+（3.14﹣π）0﹣（5 ﹣3）+2sin30°18. 解不等式： ，并在数轴上表示出它的解集19. 如图，已知在平面直角坐标系内，点A（1，﹣4），点B（3，3），点C（5，1）
(1)、①画出△ABC；②画出△ABC关于y轴对称的△A1B1C1；
(2)、求四边形ABB1A1的面积.20. 近几年购物的支付方式日益增多，某数学兴趣小组就此进行了抽样调查．调查结果显示，支付方式有：A微信、B支付宝、C现金、D其他，该小组对某超市一天内购买者的支付方式进行调查统计，得到如下两幅不完整的统计图．
请你根据统计图提供的信息，解答下列问题：
(1)、本次一共调查了多少名购买者？(2)、请补全条形统计图；在扇形统计图中A种支付方式所对应的圆心角为度．(3)、若该超市这一周内有1600名购买者，请你估计使用A和B两种支付方式的购买者共有多少名？21. 如图，在菱形ABCD中，取CD中点O，以O为圆心OD为半径作圆交AD于E交BC的延长线交于点F，AB＝4，BE＝5，连结OB
(1)、求DE的长；(2)、求tan∠OBC的值.22. 如图是集体跳绳的示意图，绳子在最高处和最低处时可以近似看作两条对称的抛物线，分别记为C1和C2 ， 绳子在最低点处时触地部分线段CD＝2米，两位甩绳同学的距离AB＝8米，甩绳的手最低点离地面高度AE＝BN＝ 米，最高点离地AF＝BM＝ 米，以地面AB、抛物线对称轴GH所在直线为x轴和y轴建立平面直角坐标系.
(1)、求抛物线C1和C2的解析式；(2)、若小明离甩绳同学点A距离1米起跳，至少要跳多少米以上才能使脚不被绳子绊住？(3)、若集体跳绳每相邻两人（看成两个点）之间最小距离为0.8米，腾空后的人的最高点头顶与最低点脚底之距为1.5米，请通过计算说明，同时进行跳绳的人数最多可以容纳几人？（温馨提醒：所有同学起跳处均在直线CD上，不考虑错时跳起问题，即身体部分均在C1和C2之间才算通过），（参考数据： ＝1.414， ≈1.732）23. 定义：若一个三角形一条边上的高长为这条边长的一半，则称该三角形为这条边上的“半高”三角形，这条高称为这条边上的“半高”，如图，△ABC是BC边上的“半高”三角形.点P在边AB上，PQ∥BC交AC于点Q，PM⊥BC于点M，QN⊥BC于点N，连接MQ.
(1)、请证明△APQ为PQ边上的“半高”三角形.(2)、请探究BM，PM，CN之间的等量关系，并说明理由；(3)、若△ABC的面积等于16，求MQ的最小值24. 在平面直角坐标系中，线段AB的两个端点A（0，2），B（1，0），点C为线段AB的中点.将线段BA绕点B按顺时针方向旋转90°得到线段BD，连结CD，AD.点P是直线BD上的一个动点.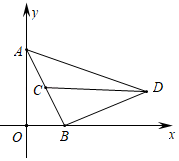
(1)、求点D的坐标和直线BD的解析式；(2)、当∠PCD＝∠ADC时，求点P的坐标；(3)、若点Q是经过点B，点D的抛物线y＝ax2+bx+2上的一个动点，请你探索：是否存在这样的点Q，使得以点P、点Q、点D为顶点的三角形与△ACD相似.若存在，请求出点P的坐标；若不存在，请说明理由.