浙江省金华市婺城区2019届数学中考模拟试卷(4月)
试卷更新日期:2019-09-03 类型:中考模拟
一、单选题
-
1. 在实数|﹣3|,﹣2,0,π中,最小的数是( )
A、|﹣3| B、﹣2 C、0 D、π2. 下列计算结果等于x3的是( )
A、x6÷x2 B、x4﹣x C、x+x2 D、x2•x3. 若一个角为65°,则它的补角的度数为( )
A、25° B、35° C、115° D、125°4. 下列图形中,哪一个是圆锥的侧面展开图?( )A、 B、
B、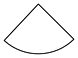 C、
C、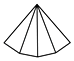 D、
D、 5. 一元一次不等式组 的解集是( )A、x>﹣1 B、x≤2 C、﹣1<x≤2 D、x>﹣1或x≤26. 解分式方程 ,去分母得( )A、 B、 C、 D、7. 如图是根据我市某天七个整点时的气温绘制成的统计图,则这七个整点时气温的中位数和平均数分别是( )
5. 一元一次不等式组 的解集是( )A、x>﹣1 B、x≤2 C、﹣1<x≤2 D、x>﹣1或x≤26. 解分式方程 ,去分母得( )A、 B、 C、 D、7. 如图是根据我市某天七个整点时的气温绘制成的统计图,则这七个整点时气温的中位数和平均数分别是( ) A、30,28 B、26,26 C、31,30 D、26,228. 如图所示,抛物线 2- 与x、y轴分别交于A,B,C三点,连结AC和BC,将△ABC沿与坐标轴平行的方向平移,若边BC的中点M落在抛物线上时,则符合条件的平移距离的值有( )
A、30,28 B、26,26 C、31,30 D、26,228. 如图所示,抛物线 2- 与x、y轴分别交于A,B,C三点,连结AC和BC,将△ABC沿与坐标轴平行的方向平移,若边BC的中点M落在抛物线上时,则符合条件的平移距离的值有( ) A、1个 B、2个 C、3个 D、4个9. 某数学研究性学习小组制作了如下的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为10的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出sin∠AOB的值是( )
A、1个 B、2个 C、3个 D、4个9. 某数学研究性学习小组制作了如下的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为10的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出sin∠AOB的值是( ) A、 B、 C、 D、10. 如图所示,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图形中“●”的个数为a1 , 第2幅图形中“●”的个数为a2 , 第3幅图形中“●”的个数为a3 , …,以此类推,则 + + +…+ 的值为( )
A、 B、 C、 D、10. 如图所示,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图形中“●”的个数为a1 , 第2幅图形中“●”的个数为a2 , 第3幅图形中“●”的个数为a3 , …,以此类推,则 + + +…+ 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 因式分解:a2-a= .12. 某桑蚕丝的直径约为0.000016,将“0.000016米”用科学记数法可表示为米.13. 小明一月底时每分钟120次,因为很快就要体育中考,所以他有意加强训练结果到三月底时每分钟已经达到180次.设二、三月份每月的平均增长率为x,根据题意列出的方程是.14. 如图所示,反比例函数y= (>0)与过点M(-2,0)的直线l:y=kx+b的图象交于A,B两点,若△ABO的面积为 ,则直线l的解析式为.
 15. 如图,正方形ABCD的边长为( +1),点M、N分别是边BC、AC上的动点,沿MN所在直线折叠正方形,使点C的对应点C'始终落在边AB上,若△NAC'为直角三角形,则CN的长为.
15. 如图,正方形ABCD的边长为( +1),点M、N分别是边BC、AC上的动点,沿MN所在直线折叠正方形,使点C的对应点C'始终落在边AB上,若△NAC'为直角三角形,则CN的长为.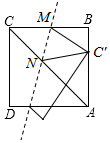 16. 某一房间内A、B两点之间设有探测报警装置,小车(不计大小)在房间内运动,当小车从AB之间经过时,将触发报警.现将A、B两点放置于平面直角坐标系xOy中(如图)已知点A,B的坐标分别为(0,4),(5,4),小车沿抛物线y=ax2-2ax-3a运动.若小车在运动过程中只触发一次报警,则a的取值范围是
16. 某一房间内A、B两点之间设有探测报警装置,小车(不计大小)在房间内运动,当小车从AB之间经过时,将触发报警.现将A、B两点放置于平面直角坐标系xOy中(如图)已知点A,B的坐标分别为(0,4),(5,4),小车沿抛物线y=ax2-2ax-3a运动.若小车在运动过程中只触发一次报警,则a的取值范围是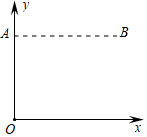
三、解答题
-
17. 计算:| -2|+20190-(- )-1+3tan30°.18. 为了丰富同学们的课余生活,某学校计划举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是?”的问卷调查,要求学“A,B,C,D“四个景点中选择一个,根据调查结果,绘制了如下两幅不完整的统计图请你根据图中所提供的信息,完成下列问题:
 (1)、本次调查的学生人数为.(2)、在扇形统计图中,景点B部分所占圆心角的度数为.(3)、若该校共有2000名学生,请估算该校最想去景点C的学生人数.19. 如图,已知反比例函数y= (k≠0)的图象过点A(-3,2).
(1)、本次调查的学生人数为.(2)、在扇形统计图中,景点B部分所占圆心角的度数为.(3)、若该校共有2000名学生,请估算该校最想去景点C的学生人数.19. 如图,已知反比例函数y= (k≠0)的图象过点A(-3,2).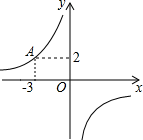 (1)、求这个反比例函数的解析式;(2)、若B(x1 , y1),C(x2 , y2),D(x3 , y3)是这个反比例函数图象上的三个点,若x1>x2>0>x3 , 请比较y1 , y2 , y3的大小,并说明理由.20. 如图,利用一幢已知高度的楼房CD(楼高为20m),来测量一幢高楼AB的高在DB上选取观测点E、F,从E测得楼房CD和高楼AB的顶部C、A的仰角分别为58°、45°.从F测得C,A的仰角分别为22°,70°.求楼AB的高度(精确到1m)(参考数据:tan22°≈0.40,tan58°≈1.60,tan70°≈2.75)
(1)、求这个反比例函数的解析式;(2)、若B(x1 , y1),C(x2 , y2),D(x3 , y3)是这个反比例函数图象上的三个点,若x1>x2>0>x3 , 请比较y1 , y2 , y3的大小,并说明理由.20. 如图,利用一幢已知高度的楼房CD(楼高为20m),来测量一幢高楼AB的高在DB上选取观测点E、F,从E测得楼房CD和高楼AB的顶部C、A的仰角分别为58°、45°.从F测得C,A的仰角分别为22°,70°.求楼AB的高度(精确到1m)(参考数据:tan22°≈0.40,tan58°≈1.60,tan70°≈2.75) 21. 如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,连接BD.
21. 如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,连接BD. (1)、求证:BG与⊙O相切;(2)、若 ,求 的值.22. 甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示
(1)、求证:BG与⊙O相切;(2)、若 ,求 的值.22. 甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示 (1)、甲的速度为千米/分,乙的速度为千米/分(2)、当乙到达终点A后,甲还需分钟到达终点B(3)、请通过计算回答:当甲、乙之间的距离为10千米时,甲出发了多少分钟?23. 如图1,△ACB为等腰直角三角形,△EDF为非等腰直角三角形,∠ACB=∠EDF=90°,且AB=EF.
(1)、甲的速度为千米/分,乙的速度为千米/分(2)、当乙到达终点A后,甲还需分钟到达终点B(3)、请通过计算回答:当甲、乙之间的距离为10千米时,甲出发了多少分钟?23. 如图1,△ACB为等腰直角三角形,△EDF为非等腰直角三角形,∠ACB=∠EDF=90°,且AB=EF.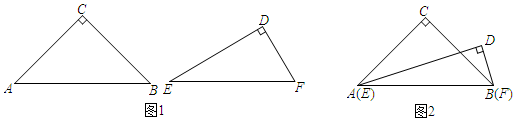 (1)、如图2,将两个直角三角形按如图2将斜边重叠摆放.当AB=EF=6,DB= 时.
(1)、如图2,将两个直角三角形按如图2将斜边重叠摆放.当AB=EF=6,DB= 时.①DA=;
②求DC的长.
(2)、若将题中两个直角三角形的斜边重叠摆放,那么线段CD、AD、BD之间存在怎样的数量关系?请直接写出答案.24. 在矩形ABCD中,∠B的角平分线BE与AD交于点E. (1)、若AB=9.
(1)、若AB=9.①如图1,过E作BE的垂线,交边CD于点F.若点F恰好是CD边的中点,则BC=;
②如图2,过E作∠BED的角平分线EF与DC交于点F,若DF=2FC,求BC的长;(结果保留根号)
(2)、如图3,分别以BC、BA直线为x、y轴,建立平面直角坐标系.若点P从点B出发,以每秒 个单位长度的速度沿射线BE方向移动;同时点Q从点B出发,以每秒2个单位长度的速度沿射线BC方向移动.设移动时间为t秒.问是否存在某一时刻t,将△PQD绕某点旋转180°后,三个对应顶点恰好都落在经过P、Q、B三点的抛物线上?若存在,求出t的值;若不存在,请说明理由.