浙江省嘉兴市秀洲区2019届数学中考一模试卷
试卷更新日期:2019-09-03 类型:中考模拟
一、单选题
-
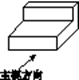
1. 的倒数是( )A、2016 B、 C、﹣2016 D、﹣2. 下列计算中,正确的是( )A、a6÷a2=a3 B、(a+1)2=a2+1 C、(﹣a)3=﹣a3 D、(ab3)2=a2b53. 现在网购越来越多地成为人们的一种消费方式,在2017年的“双11”促销活动中,天猫和淘宝的支付交易额突破,将1682亿元用科学记数法表示为( )元.A、0.1682×1011 B、1.682×1011 C、1.682×1012 D、1682×1084. 如图所示的几何体的主视图为( )
 A、
A、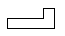 B、
B、 C、
C、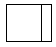 D、
D、 5. 若点A(m,n)和点B(5,﹣7)关于x轴对称,则m+n的值是( )A、2 B、﹣2 C、12 D、﹣126.
5. 若点A(m,n)和点B(5,﹣7)关于x轴对称,则m+n的值是( )A、2 B、﹣2 C、12 D、﹣126.如图,直线l1∥l2 , 以直线l1上的点A为圆心、适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC.若∠ABC=67°,则∠1=( )
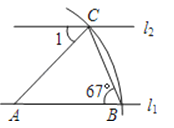 A、23° B、46° C、67° D、78°7. 已知反比例函数 的图象,在每一象限内, 的值随 值的增大而减少,则一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 用圆心角为120°,半径为6 cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )
A、23° B、46° C、67° D、78°7. 已知反比例函数 的图象,在每一象限内, 的值随 值的增大而减少,则一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 用圆心角为120°,半径为6 cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( ) A、 cm B、3 cm C、4 cm D、4 cm9. 若数 使关于 的分式方程 的解为正数,且使关于 的不等式组 的解集为 ,则符合条件的所有整数 的和为( )A、10 B、12 C、14 D、1610. 滴滴快车是一种便捷的出行工具,计价规则如下表:
A、 cm B、3 cm C、4 cm D、4 cm9. 若数 使关于 的分式方程 的解为正数,且使关于 的不等式组 的解集为 ,则符合条件的所有整数 的和为( )A、10 B、12 C、14 D、1610. 滴滴快车是一种便捷的出行工具,计价规则如下表:计费项目
里程费
时长费
远途费
单价
1.8元/公里
0.3元/分钟
0.8元/公里
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7公里以内(含7公里)不收远途费,超过7公里的,超出部分每公里收0.8元.
小王与小张各自乘坐滴滴快车,行车里程分别为6公里与8.5公里.如果下车时两人所付车费相同,那么这两辆滴滴快车的行车时间相差( )
A、10分钟 B、13分钟 C、15分钟 D、19分钟二、填空题
-
11. 若x是3和6的比例中项,则x=.12. 分解因式:x2﹣4= .13. 已知二次函数y=ax2+bx﹣3自变量x的部分取值和对应函数值y如下表:
则在实数范围内能使得y﹣5>0成立的x取值范围是.
x
…
﹣2
﹣1
0
1
2
3
…
y
…
5
0
﹣3
﹣4
﹣3
0
…
14. 如图所示,一个宽为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么该光盘的直径是cm. 15. 如图,在平面直角坐标系中,点A(4 ,0)是x轴上一点,以OA为对角线作菱形OBAC,使得∠BOC.=60°,现将抛物线y=x2沿直线OC平移到y=a(x﹣m)2+h,那么h关于m的关系式是 , 当抛物线与菱形的AB边有公共点时,则m的取值范围是.
15. 如图,在平面直角坐标系中,点A(4 ,0)是x轴上一点,以OA为对角线作菱形OBAC,使得∠BOC.=60°,现将抛物线y=x2沿直线OC平移到y=a(x﹣m)2+h,那么h关于m的关系式是 , 当抛物线与菱形的AB边有公共点时,则m的取值范围是. 16. 如图,已知在平面直角坐标系中,点A(0,3),点B为x轴上一动点,连接AB,线段AB绕着点B按顺时针方向旋转90°至线段CB,过点C作直线l∥y轴,在直线l上有一点D位于点C下方,满足CD=BO,则当点B从(﹣3,0)平移到(3,0)的过程中,点D的运动路径长为.
16. 如图,已知在平面直角坐标系中,点A(0,3),点B为x轴上一动点,连接AB,线段AB绕着点B按顺时针方向旋转90°至线段CB,过点C作直线l∥y轴,在直线l上有一点D位于点C下方,满足CD=BO,则当点B从(﹣3,0)平移到(3,0)的过程中,点D的运动路径长为.
三、解答题
-
17.(1)、计算:(2)、解方程:x2﹣2x﹣9=018. 国学经典进校园,传统文化润心灵,某校开设了“围棋入门”、“诗歌汉字”、“翰墨飘香”、“史学经典”四门拓展课(每位学生必须且只选其中一门).(1)、学校对八年级部分学生进行选课调查,
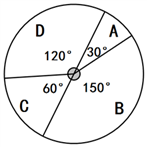

得到如图所示的统计图,请估计该校八年级420名学生选“诗歌汉字”的人数.
(2)、“翰墨飘香”书画社的甲、乙、丙三人的书法水平相当,学校决定从这三名同学中任选两名参加市书法比赛,求甲和乙被选中的概率.(要求列表或画树状图)19. 如图,在方格纸中,点A,D都在格点上,作三角形ABC,使其满足下列条件.(点B,C不与点D重合) (1)、在图甲中,作格点等腰△ABC,使AD为△ABC的高线.(2)、在图乙中,作格点钝角△ABC,使AD为△ABC的角平分线20. 如图,已知△ABC内接于⊙O,AB为⊙O的直径,BD⊥AB,交AC的延长线于点D.
(1)、在图甲中,作格点等腰△ABC,使AD为△ABC的高线.(2)、在图乙中,作格点钝角△ABC,使AD为△ABC的角平分线20. 如图,已知△ABC内接于⊙O,AB为⊙O的直径,BD⊥AB,交AC的延长线于点D. (1)、E为BD的中点,连结CE,求证:CE是⊙O的切线;(2)、若AC=3CD,求∠A的大小.21. 如图,一扇窗户垂直打开,即OM⊥OP , AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端C在OP上滑动,将窗户OM按图示方向向内旋转37°到达ON位置,此时,点A、C的对应位置分别是点B、D.测量出∠ODB为28°,点D到点O的距离为30cm .
(1)、E为BD的中点,连结CE,求证:CE是⊙O的切线;(2)、若AC=3CD,求∠A的大小.21. 如图,一扇窗户垂直打开,即OM⊥OP , AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端C在OP上滑动,将窗户OM按图示方向向内旋转37°到达ON位置,此时,点A、C的对应位置分别是点B、D.测量出∠ODB为28°,点D到点O的距离为30cm . (1)、求B点到OP的距离;(2)、求滑动支架的长.(结果精确到0.1)(数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53,sin 53°≈0.8,cos53°≈0.6,tan53°≈1.33)22. 某商场计划购进A,B两种新型节能台灯共100盏,这两种台灯的进价、售价如下表:
(1)、求B点到OP的距离;(2)、求滑动支架的长.(结果精确到0.1)(数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53,sin 53°≈0.8,cos53°≈0.6,tan53°≈1.33)22. 某商场计划购进A,B两种新型节能台灯共100盏,这两种台灯的进价、售价如下表:类型
价格
进价(元/盏)
售价(元/盏)
A型
30
45
B型
50
70
(1)、若商场预计进货款为3500元,则这两种台灯各进多少盏.(2)、若设商场购进A型台灯m盏,销售完这批台灯所获利润为P,写出P与m之间的函数关系式.(3)、若商场规定B型灯的进货数量不超过A型灯数量的4倍,那么A型和B型台灯各进多少盏售完之后获得利润最多?此时利润是多少元.23. 如图1,在△ABC中,点P为边AB所在直线上一点,连结CP,M为线段CP的中点,若满足∠ACP=∠MBA,则称点P为△ABC的“好点”. (1)、如图2,当∠ABC=90°时,命题“线段AB上不存在“好点”为(填“真”或“假”)命题,并说明理由;(2)、如图3,P是△ABC的BA延长线的一个“好点”,若PC=4,PB=5,求AP的值;(3)、如图4,在Rt△ABC中,∠CAB=90°,点P是△ABC的“好点”,若AC=4,AB=5,求AP的值.24. 如图①,在平面直角坐标系中,二次函数y=﹣ x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
(1)、如图2,当∠ABC=90°时,命题“线段AB上不存在“好点”为(填“真”或“假”)命题,并说明理由;(2)、如图3,P是△ABC的BA延长线的一个“好点”,若PC=4,PB=5,求AP的值;(3)、如图4,在Rt△ABC中,∠CAB=90°,点P是△ABC的“好点”,若AC=4,AB=5,求AP的值.24. 如图①,在平面直角坐标系中,二次函数y=﹣ x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ. (1)、填空:b= , c=;(2)、在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;(3)、在x轴下方,该二次函数的图象上是否存在点M,使△PQM是以点P为直角顶点的等腰直角三角形?若存在,请求出运动时间t;若不存在,请说明理由;(4)、如图②,点N的坐标为(﹣ ,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.
(1)、填空:b= , c=;(2)、在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;(3)、在x轴下方,该二次函数的图象上是否存在点M,使△PQM是以点P为直角顶点的等腰直角三角形?若存在,请求出运动时间t;若不存在,请说明理由;(4)、如图②,点N的坐标为(﹣ ,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.