浙江省杭州市下城区2019届数学中考二模试卷
试卷更新日期:2019-09-03 类型:中考模拟
一、单选题
-
1. -2+3=( )A、1 B、-1 C、5 D、-52. 用科学记数法表示23000为( )A、 B、 C、 D、3. 16的平方根为( )A、 ±4 B、±2 C、+4 D、24. 若数组2,2,x,3,4的平均数为3,则这组数中的( )A、x=3 B、中位数为3 C、众数为3 D、中位数为x5. 若x>y,a<1,则( )A、x>y+1 B、x+1>y+a C、ax>ay D、x-2>y-16. 今年父亲的年龄是儿子年龄的3倍,5年前父亲的年龄是儿子年龄的4倍.设今年儿子的年龄为x岁,则下列式子正确的是( )A、4x-5=3(x-5) B、4x+5=3(x+5) C、3x+5=4(x+5) D、3x-5=4(x-5)7. 如图是一个游戏转盘,自由转动转盘,当转盘停止后,若指针落在所示区域内事件发生的概率依次记为r,s,t,k,则( )
 A、 B、 C、 D、8. 如图,在∆ABC中,AC=BC,过C作CD//AB.若AD平分∠CAB,则下列说法错误的是( )
A、 B、 C、 D、8. 如图,在∆ABC中,AC=BC,过C作CD//AB.若AD平分∠CAB,则下列说法错误的是( ) A、BC=CD B、BO:OC=AB:BC C、△CDO≌△BAO D、9. 四位同学在研究函数 (a,b,c是常数)时,甲发现当x=-1时函数的最小值为-1;乙发现4a-2b+c=0成立;丙发现当x<1时,函数值y随x的增大而增大;丁发现当x=5时,y=-4.已知这四位同学中只有一位发现的结论是错误的,则该同学是( )A、甲 B、乙 C、丙 D、丁10. 如图,AB为 的直径,P为BA延长线上的一点,D在 上(不与点A,点B重合),连结PD交 于点C,且PC=OB.设 ,下列说法正确的是( )
A、BC=CD B、BO:OC=AB:BC C、△CDO≌△BAO D、9. 四位同学在研究函数 (a,b,c是常数)时,甲发现当x=-1时函数的最小值为-1;乙发现4a-2b+c=0成立;丙发现当x<1时,函数值y随x的增大而增大;丁发现当x=5时,y=-4.已知这四位同学中只有一位发现的结论是错误的,则该同学是( )A、甲 B、乙 C、丙 D、丁10. 如图,AB为 的直径,P为BA延长线上的一点,D在 上(不与点A,点B重合),连结PD交 于点C,且PC=OB.设 ,下列说法正确的是( )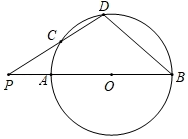 A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则
A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则二、填空题
-
11. .12. 如图,若 ,则∠1的度数为.
 13. 若多项式A满足, ,则A=.14. 已知C是优弧AB的中点,若 ,则AB=.
13. 若多项式A满足, ,则A=.14. 已知C是优弧AB的中点,若 ,则AB=.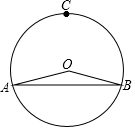 15. 函数 和函数 的图象交于点 ,若 ,则x的取值范围为.16. 如图,在∆ABC中,AB=AC=10,E,D分别是AB,AC上的点,BE=4,CD=2,且BD=CE,则BD=.
15. 函数 和函数 的图象交于点 ,若 ,则x的取值范围为.16. 如图,在∆ABC中,AB=AC=10,E,D分别是AB,AC上的点,BE=4,CD=2,且BD=CE,则BD=.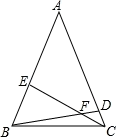
三、解答题
-
17. 在等腰三角形ABC中,底边BC为y,腰长AB长为x,若三角形ABC的周长为12.(1)、求y关于x的函数表达式;(2)、当腰长比底边的2倍多1时,求x的值.18. 为了解八年级学生双休日的课外阅读情况,学校随机调查了该年级25名学生,得到了一组样本数据,其统计表如下:
八年级25名学生双休日课外阅读时间统计表
阅读时间
1小时
2小时
3小时
4小时
5小时
6小时
人数
3
4
6
3
2
(1)、请求出阅读时间为4小时的人数所占百分比;(2)、试确定这个样本的众数和平均数.19. 如图,直线 ,AC分别交 于点A,B,C;DF分别交 于点D,E,F;AC与DF交于点O.已知DE=3,EF=6,AB=4. (1)、求AC的长;(2)、若BE:CF=1:3,求OB:AB.20. 如图,过点P作PA,PB,分别与以OA为半径的半圆切于A,B,延长AO交切线PB于点C,交半圆与于点D.
(1)、求AC的长;(2)、若BE:CF=1:3,求OB:AB.20. 如图,过点P作PA,PB,分别与以OA为半径的半圆切于A,B,延长AO交切线PB于点C,交半圆与于点D. (1)、若PC=5,AC=4,求BC的长;(2)、设DC:AD=1:2,求 的值.21. 在平面直角坐标系中,反比例函数 (k是常数,且 )的图象经过点 .(1)、若b=4,求y关于x的函数表达式;(2)、点 也在反比例函数y的图象上:
(1)、若PC=5,AC=4,求BC的长;(2)、设DC:AD=1:2,求 的值.21. 在平面直角坐标系中,反比例函数 (k是常数,且 )的图象经过点 .(1)、若b=4,求y关于x的函数表达式;(2)、点 也在反比例函数y的图象上:①当 且 时,求b的取值范围;
②若B在第二象限,求证: .
