浙江省绍兴市诸暨市2018-2019学年八年级下学期数学期末考试卷

试卷更新日期：2019-09-03 类型：期末考试

进入出卷网下载

一、选择题（本大题有10小题，每小题3分，共30分.）

1. 若二次根式 $\sqrt{x - 4}$ 有意义，则x的取值范围是（）

A、x＜4 B、x＞4 C、x≥4 D、x≤4

查看试题解析
2. 下列图形中，既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. 某校九年级“诗歌大会”比赛中，各班代表队得分如下（单位：分）：9，7，8，7，9，7，6，则各代表队得分的中位数是（）

A、9分 B、8分 C、7分 D、6分

查看试题解析
4. 若关于x的一元二次方程x²﹣3x+m＝0有解，则m的值可为（）

A、2 B、3 C、4 D、5

查看试题解析
5. 下列各式中计算正确的是（）

A、 $\sqrt{2}$ + $\sqrt{3}$ ＝ $\sqrt{5}$ B、 $\sqrt{\frac{3}{4}}$ ＝ $\frac{\sqrt{3}}{2}$ C、 $\sqrt{3^{2} + 4^{2}} = 3 + 4 = 7$ D、（ $\sqrt{3}$ + $\sqrt{2}$ ）²＝3+2＝5

查看试题解析
6. 已知：如图，M是正方形ABCD内的一点，且MC＝MD＝AD，则∠AMB的度数为（）

A、120° B、135° C、145° D、150°

查看试题解析
7. 下图入口处进入，最后到达的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
8. 如图，空地上（空地足够大）有一段长为20m的旧墙MN，小敏利用旧墙和木栏围成一个矩形菜园ABCD，已知木栏总长100m，矩形菜园ABCD的面积为900m² ．若设AD＝xm，则可列方程（）

A、（50﹣ $\frac{x}{2}$ ）x＝900 B、（60﹣x）x＝900 C、（50﹣x）x＝900 D、（40﹣x）x＝900

查看试题解析
9. 如图1是由5个全等的边长为1的正方形拼成的图形，现有两种不同的方式将它沿着虚线剪开，甲将它分成三块，乙将它分成四块，各自要拼一个面积是5的大正方形，则（）

A、甲、乙都可以 B、甲可以，乙不可以 C、甲不可以，乙可以 D、甲、乙都不可以

查看试题解析
10. 已知：如图，在菱形OABC中，OC＝8，∠AOC＝60°，OA落在x轴正半轴上，点D是OC边上的一点（不与端点O，C重合），过点D作DE⊥AB于点E，若点D，E都在反比例函数y＝ $\frac{k}{x}$ （x＞0）图象上，则k的值为（）

A、8 $\sqrt{3}$ B、9 C、9 $\sqrt{3}$ D、16

查看试题解析

二、填空题（本大题有10小题，每小题3分，共30分）

11. 计算： $\sqrt{{(- 2)}^{2}}$ ＝．

查看试题解析
12. 在反比例函数 $y = \frac{m - 2}{x}$ 的图象每一条曲线上，y都随x的增大而减小，则m的取值范围是．

查看试题解析
13. 用反证法证明“若|a|＜2，则a²＜4”时，应假设．

查看试题解析
14. 甲，乙，丙，丁四人参加射击测试，每人10次射击的平均环数都为8.9环，各自的方差见如下表格

甲

乙

丙

丁

方差

0.293

0.375

0.362

0.398

则四个人中成绩最稳定的是．

查看试题解析
15. 一个多边形的每个内角都等于150°，则这个多边形是边形．

查看试题解析
16. 如图，在▱ABCD中，对角线AC与BD相交于点O，E是边CD的中点，连结OE．若∠ABC＝60，∠BAC＝80°，则∠1的度数为．

查看试题解析
17. 三角形的两边长为2和4，第三边长是方程x²﹣6x+8=0的根，则这个三角形的周长是．

查看试题解析
18. 为预防传染病，某校定期对教室进行“药熏消毒”，已知药物燃烧阶段，室内每立方米空气中的含药量y（mg）与燃烧时间x（分钟）成正比例；燃烧后，y与x成反比例（如图所示）．现测得药物10分钟燃烧完，此时教室内每立方米空气含药量为6mg．研究表明当每立方米空气中含药量低于1.2mg时，对人体方能无毒害作用，那么从消毒开始，至少需要经过分钟后，学生才能回到教室．

查看试题解析
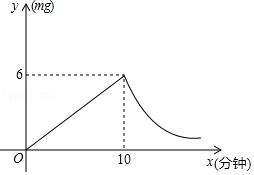19. 如图，在矩形ABCD内放入四个小正方形和两个小长方形后成中心对称图形，其中顶点E，F分别在边AD，BC上，小长方形的长与宽的比值为4，则 $\frac{A D}{A B}$ 的值为．

查看试题解析
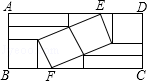20. 在矩形ABCD中，AB＝3，点E是BC的中点，将△ABE沿AE折叠后得到△AFE，点B的对应点为点F．

(1)、若点F恰好落在AD边上，则AD＝．

(2)、延长AF交直线CD于点P，已知 $\frac{P D}{C D}$ ＝ $\frac{1}{3}$ ，则AD＝．

查看试题解析

三、解答题（本大题有5小题，第21小题6分，第22～24小题8分，第25小题10分，共40分.）

21.

(1)、计算：（2﹣ $\sqrt{3}$ ）（2+ $\sqrt{3}$ ）﹣（ $\sqrt{5}$ ）² ．

(2)、解方程：x²﹣4x+1＝0．

查看试题解析
22. 某中学开展的“好书伴我成长”读书活动中，为了解七年级600名学生读书情况，随机调查了七年级50名学生读书的册数，统计数据如下表所示：

册数

0

1

2

3

4

人数

3

13

16

17

1

(1)、这50个样本数据的众数为、中位数为；

(2)、求这50个样本数据的平均数；

(3)、根据样本数据，估计该校七年级600名学生在本次活动中读书多于2册的人数．

查看试题解析
23. 如图，矩形ABCD中，点E、F分别在边CD、AB上，且DE＝BF．

(1)、求证：四边形AFCE是平行四边形．

(2)、若四边形AFCE是菱形，AB＝8，AD＝4，求菱形AFCE的周长．

查看试题解析
24. 如图，平面直角坐标系xOy中，函数y＝ $\frac{k}{x}$ （x＜0）的图象经过点A（﹣1，6），直线y＝mx﹣2与x轴交于点B（﹣1，0）．

(1)、求k，m的值．

(2)、点P是直线y＝﹣2x位于第二象限上的一个动点，过点P作平行于x轴的直线，交直线y＝mx﹣2于点C，交函数y＝ $\frac{k}{x}$ （x＜0）的图象于点D，设P（n，﹣2n）．
①当n＝﹣1时，判断线段PD与PC的数量关系，并说明理由

②当PD≥2PC时，结合函数的图象，直接写出n的取值范围．

查看试题解析
25. 如图，以矩形OABC的顶点O为坐标原点，OA所在直线为x轴，OC所在直线为y轴，建立平面直角坐标系，已知OA＝8，OC＝10，将矩形OABC绕点O逆时针方向旋转α（0＜α＜180°）得到矩形ODEF．

(1)、当点E恰好落在y轴上时，如图1，求点E的坐标．

(2)、连结AC，当点D恰好落在对角线AC上时，如图2，连结EC，EO，
①求证：△ECD≌△ODC；

②求点E的坐标．

(3)、在旋转过程中，点M是直线OD与直线BC的交点，点N是直线EF与直线BC的交点，若BM＝ $\frac{1}{2}$ BN，请直接写出点N的坐标．

查看试题解析

	甲	乙	丙	丁
方差	0.293	0.375	0.362	0.398

册数	0	1	2	3	4
人数	3	13	16	17	1