云南省昭通市2018-2019学年七年级下学期数学期末考试卷

试卷更新日期：2019-09-03 类型：期末考试

进入出卷网下载

一、填空题（本大题共6小題，共18分）

1.
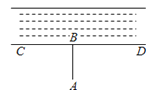
如图，计划把河水引到水池A中，先作AB⊥CD，垂足为B，然后沿AB开渠，能使所开的渠道最短，这样设计的依据是

查看试题解析
2. 写出一个以 ${\begin{matrix} x = 2 \\ y = - 3 \end{matrix}$ 为解的二元一次方程组．（答案不唯一）

查看试题解析
3. 已经点P（a+2，a﹣1）在平面直角坐标系的第四象限，则a的取值范围是

查看试题解析
4. 在高3米，水平距离为4米的楼梯表面铺地毯，地毯的长度至少需要米．

查看试题解析
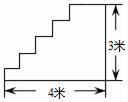5. 已知a为 $\sqrt{17}$ 的整数部分，b﹣1是400的算术平方根，则 $\sqrt{a + b}$ 的值为．

查看试题解析
6. 若不等式组 ${\begin{matrix} x > - 3 \\ x < a \end{matrix}$ 无解，则a的取值范围是．

查看试题解析

二、选择题（本大题共8小题，共32分）

7. 36的算术平方根是（）

A、 6 B、﹣6 C、±6 D、 $\sqrt{6}$

查看试题解析
8. 通过平移，可将如图中的福娃“欢欢”移动到图（）

A、 B、 C、 D、

查看试题解析
9. 在平面直角坐标系中，点（2018，﹣ $\sqrt{2}$ ）所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
10. 在实数 $\frac{22}{7}$ ，0.1010010001…， $\sqrt[3]{8}$ ，﹣π， $\sqrt{3}$ 中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 一次中考考试中考生人数为15万名，从中抽取6000名考生的中考成绩进行分析，在这个问题中样本指的是（）

A、6000 B、6000名考生的中考成绩 C、15万名考生的中考成绩 D、6000名考生

查看试题解析
12. 如图所示，点E在AC的延长线上，下列条件中能判断AB∥CD的是（）

A、∠3＝∠4 B、∠1＝∠2 C、∠D＝∠DCE D、∠D+∠ACD＝180°

查看试题解析
13. 一架飞机在两城间飞行，顺风航行要5.5小时，逆风航行要6小时，风速为24千米/时，设飞机无风时的速度为每小时x千米，则下列方程正确是（）

A、5.5（x﹣24）=6（x+24） B、 $\frac{x - 24}{5.5}$ = $\frac{x + 24}{6}$ C、5.5（x+24）=6（x﹣24） D、 $\frac{2 x}{5.5 + 6}$ = $\frac{x}{5.5}$ ﹣24

查看试题解析
14. 已知关于x，y的方程组 ${\begin{matrix} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{matrix}$ 的解 ${\begin{matrix} x = 3 \\ y = 2 \end{matrix}$ ．则关于x，y的方程组 ${\begin{matrix} a_{1} (x - 1) - b_{1} y = c_{1} \\ a_{2} (x - 1) - b_{2} y = c_{2} \end{matrix}$ 的解是（）

A、 ${\begin{matrix} x = 4 \\ y = - 2 \end{matrix}$ B、 ${\begin{matrix} x = 1 \\ y = 2 \end{matrix}$ C、 ${\begin{matrix} x = 3 \\ y = - 2 \end{matrix}$ D、 ${\begin{matrix} x = 4 \\ y = 2 \end{matrix}$

查看试题解析

三、解答题（70分）

15. 计算： $\sqrt{4}$ + $\sqrt[3]{- \frac{1}{8}}$ + $\sqrt{{(- \frac{1}{2})}^{2}}$

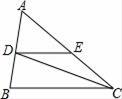
查看试题解析
16. 解二元一次方程组： ${\begin{matrix} 2 x - y = - 4 \\ 5 x + 4 y = 3 \end{matrix}$

查看试题解析
17. 解不等式组 ${\begin{matrix} 7 x - 1 > 3 (x + 1) \\ \frac{x - 3}{2} \leq 1 - \frac{x}{3} \end{matrix}$ ，并将它的解集在数轴上表示出来．

查看试题解析
18. 如图，CD平分∠ACB，DE∥BC，∠AED＝46°，求∠CDE的度数．

查看试题解析
19. 如图，在平面直角坐标系中，已知点A（﹣3，4），B（﹣4，2），C（﹣2，0），且点P（a，b）是三角形ABC边上的任意一点，三角形ABC经过平移后得到三角形A₁B₁C₁ ，点P（a，b）的对应点P₁（a+6，b﹣3）．

(1)、直接写出A₁的坐标；

(2)、在图中画出三角形A₁B₁C₁；

(3)、求出三角形ABC的面积．

查看试题解析

20. 某校举行“汉字听写”比赛，每位学生听写汉字39个比赛结束后，随机抽查部分学生的听写结果，以下是根据抽査结果绘制的统计图的一部分根据信息解决下列问题：

组别	正确字数x	人数
A	0≤x＜8	8
B	8≤x＜16	12
C	16≤x＜24	20
D	24≤x＜32	a
E	32≤x＜40	16

(1)、样本容量是， a＝， b＝；

(2)、在扇形统计图中，“D组”所对应的圆心角的度数为；

(3)、补全条形统计图；

(4)、该校共有1200名学生，如果听写正确的个数少于16个定为不合格，请你估计这所学校本次比赛听写不合格的学生人数．

查看试题解析

21. 某商店需要购进甲、乙两种商品共130件，其进价和获利情况如下表：

甲

乙

进价（元/件）

15

30

获利（元/件）

6

10

(1)、若商店计划销售完这批商品后能获利1100元，问甲、乙两种商品应分别购进多少件？

(2)、若商店计划投入资金少于3000元，且销售完这批商品后总获利多于1048元，请问有哪些购货方案？

查看试题解析
22. 如图，点E在直线DF上，点B在直线AC上，若∠1＝∠2、∠C＝∠D，试判断∠A与∠F的关系，并说明理由．

查看试题解析
23. 已知AB∥CD，点E为平面内一点，BE⊥CE于E．

(1)、如图1，请直接写出∠ABE和∠DCE之间的数量关系；

(2)、如图2，过点E作EF⊥CD，垂足为F，求证：∠CEF＝∠ABE；

(3)、如图3，在（2）的条件下，作EG平分∠CEF，交DF于点G，作ED平分∠BEF，交CD于D，连接BD，若∠DBE+∠ABD＝180°，且∠BDE＝3∠GEF，求∠BEG的度数．

查看试题解析

	甲	乙
进价（元/件）	15	30
获利（元/件）	6	10