广西钦州市2018-2019学年七年级下学期数学期末考试卷
试卷更新日期:2019-09-03 类型:期末考试
一、选择题(本大题共12小题,每小题3分,共36分。)
-
1. 8的立方根是( )A、 B、±2 C、2 D、42. 点A(﹣3,4)所在象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列调查中,适合用全面调查方式的是( )A、了解市场上酸奶的质量情况 B、了解一批签字笔的使用寿命情况 C、了解某条河流的水质情况 D、了解某校七年级甲班学生期中数学考试的成绩4. 若不等式组的解集为﹣1≤x≤3,则图中表示正确的是( )A、
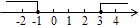 B、
B、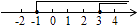 C、
C、 D、
D、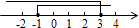 5. 如图,点E在AB的延长线上,下列条件能判断AD∥BC的是( )
5. 如图,点E在AB的延长线上,下列条件能判断AD∥BC的是( )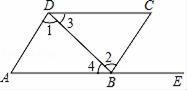 A、∠A+∠ADC=180° B、∠3=∠4 C、∠1=∠2 D、∠C=∠CBE6. 如图,数轴上点P表示的数可能是( )
A、∠A+∠ADC=180° B、∠3=∠4 C、∠1=∠2 D、∠C=∠CBE6. 如图,数轴上点P表示的数可能是( ) A、 B、 C、 D、7. 在平面直角坐标系中,将A(3,﹣1)先向左平移3个单位,再向上平移2个单位后得到点A,则A的坐标是( )A、(6,1) B、(0,1) C、(0,﹣3) D、(6,﹣3)8. 已知 是方程kx+2y=5的一个解,则k的值为( )A、﹣ B、 C、﹣ D、9. 不等式组 的最大正整数解为( )A、1 B、2 C、3 D、410. 有以下四个命题,其中正确的是( )A、同位角相等 B、0.01是0.1的一个平方根 C、若点P(x,y)在坐标轴上,则xy=0 D、若a2>b2 , 则a>b11. 在某校举办的足球比赛中规定:胜一场得3分,平一场得1分,负一场得0分.某班足球队参加了12场比赛,共得22分,已知这个队只输了2场,为求此胜几场和平几场.设这支足球队胜x场,平y场.根据题意,列出如下四个方程组,其中正确的是( )A、 B、 C、 D、12. 如图,直线AB、CD相交于点O,OD平分∠BOF,OE⊥CD于O,若∠EOF=α,下列说法①∠AOC=α﹣90°;②∠EOB=180°﹣α;③∠AOF=360°﹣2α,其中正确的是( )
A、 B、 C、 D、7. 在平面直角坐标系中,将A(3,﹣1)先向左平移3个单位,再向上平移2个单位后得到点A,则A的坐标是( )A、(6,1) B、(0,1) C、(0,﹣3) D、(6,﹣3)8. 已知 是方程kx+2y=5的一个解,则k的值为( )A、﹣ B、 C、﹣ D、9. 不等式组 的最大正整数解为( )A、1 B、2 C、3 D、410. 有以下四个命题,其中正确的是( )A、同位角相等 B、0.01是0.1的一个平方根 C、若点P(x,y)在坐标轴上,则xy=0 D、若a2>b2 , 则a>b11. 在某校举办的足球比赛中规定:胜一场得3分,平一场得1分,负一场得0分.某班足球队参加了12场比赛,共得22分,已知这个队只输了2场,为求此胜几场和平几场.设这支足球队胜x场,平y场.根据题意,列出如下四个方程组,其中正确的是( )A、 B、 C、 D、12. 如图,直线AB、CD相交于点O,OD平分∠BOF,OE⊥CD于O,若∠EOF=α,下列说法①∠AOC=α﹣90°;②∠EOB=180°﹣α;③∠AOF=360°﹣2α,其中正确的是( ) A、①② B、①③ C、②③ D、①②③
A、①② B、①③ C、②③ D、①②③二、填空题(本大题共6小题,每小题3分,共18分)
-
13. 在实数 ,﹣3, ,π中,无理数是 .14. 有30个数据,其中最大值为40,最小值为19,若取组距为4,则应该分成组.15. 如图,直线a,b被直线c所截,且a∥b.若∠1=125°,则∠2的大小为 .
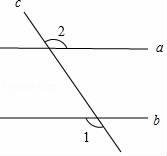 16. 若x,y为实数,且满足 +(2y+2)2=0,则(2x+y)2019的结果为 .17. 已知某品牌电烤箱进价500元/台,标价为800元/台,某商场端午节打折促销,但要保持利润率不低于20%,则最低可打折.18. 如图,在平面直角坐标系中,点A的坐标为(1,0),点A第1次跳动至点A1(﹣1,1),第2次向右跳动3个单位长度至点A2(2,1),第3次跳动至点A3(﹣2,2),第4次向右跳动5个单位长度至点A4(3,2),…,依此规律跳动下去,第100次跳动至点A100的坐标是 .
16. 若x,y为实数,且满足 +(2y+2)2=0,则(2x+y)2019的结果为 .17. 已知某品牌电烤箱进价500元/台,标价为800元/台,某商场端午节打折促销,但要保持利润率不低于20%,则最低可打折.18. 如图,在平面直角坐标系中,点A的坐标为(1,0),点A第1次跳动至点A1(﹣1,1),第2次向右跳动3个单位长度至点A2(2,1),第3次跳动至点A3(﹣2,2),第4次向右跳动5个单位长度至点A4(3,2),…,依此规律跳动下去,第100次跳动至点A100的坐标是 .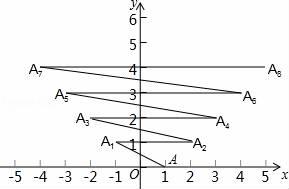
三、解答题(本大题共8小题,共66分。)
-
19. 计算: + ﹣( ﹣1).20. 解方程组:21. 解不等式组 ,并把它的解集在数轴上表示出来.
 22. 如图,在边长为1个单位长度的小正方形组成的方格纸中,△ABC的顶点都在方格纸的格点上.
22. 如图,在边长为1个单位长度的小正方形组成的方格纸中,△ABC的顶点都在方格纸的格点上.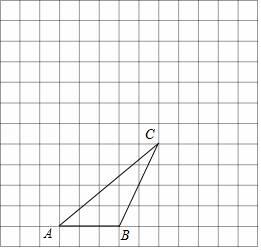 (1)、①将△ABC向右平移2个单位,得到△A1B1C1 . 请画出△A1B1C1;
(1)、①将△ABC向右平移2个单位,得到△A1B1C1 . 请画出△A1B1C1;②将△A1B1C1再向上平移5个单位得△A2B2C2 , 请画出△A2B2C2;
(2)、求△ABC的面积.23. 如图,已知∠A=∠F,∠C=∠E,求证:BE∥CD. 24. 某学校的数学小组将七年级学生某个星期天阅读时间t(单位:分钟)的调查数据进行整理,绘制出如下不完整的频数分布表和频数分布直方图;
24. 某学校的数学小组将七年级学生某个星期天阅读时间t(单位:分钟)的调查数据进行整理,绘制出如下不完整的频数分布表和频数分布直方图;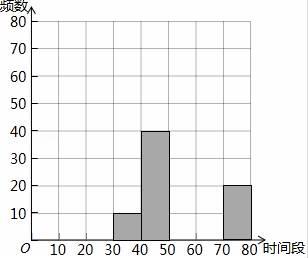
阅读时间分钟
频数(人数)
频率
30≤t<40
10
5%
40≤t<50
40
m
50≤t<60
a
40%
60≤t<70
b
n
70≤t<80
20
10%
(1)、求a= , b= , m= , n=;(2)、补全频数分布直方图;(3)、如果阅读时间不少于60分钟即为达标,则达标人数共有多少人?若七年级学生在某时间段内阅读的人数有500人,估计约有多少人达标?25. 已知AB∥CD,在AB,CD内有一条折线EGF.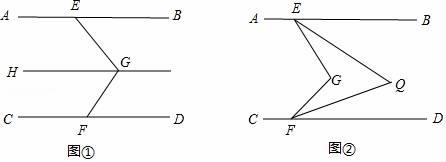 (1)、如图①,过点G作GH∥AB,求证:∠BEG+∠DFG=∠EGF;(2)、如图②,已知∠BEG的平分线与∠DFG的平分线相交于点Q,请探究∠EGF与∠EQF的数量关系,并说明理由.26. 为了响应“绿水青山就是金山银山”的环保建设,提高企业的治污能力某大型企业准备购买A,B两种型号的污水处理设备共8台,若购买A型设备2台,B型设备3台需34万元;购买A型设备4台,B型设备2台需44万元.(1)、求A,B两种型号的污水处理设备的单价各是多少?(2)、已知一台A型设备一个月可处理污水220吨,B型设备一个月可处理污水190吨,若该企业每月处理的污水不低于1700吨,请你为该企业设计一种最省钱的购买方案.
(1)、如图①,过点G作GH∥AB,求证:∠BEG+∠DFG=∠EGF;(2)、如图②,已知∠BEG的平分线与∠DFG的平分线相交于点Q,请探究∠EGF与∠EQF的数量关系,并说明理由.26. 为了响应“绿水青山就是金山银山”的环保建设,提高企业的治污能力某大型企业准备购买A,B两种型号的污水处理设备共8台,若购买A型设备2台,B型设备3台需34万元;购买A型设备4台,B型设备2台需44万元.(1)、求A,B两种型号的污水处理设备的单价各是多少?(2)、已知一台A型设备一个月可处理污水220吨,B型设备一个月可处理污水190吨,若该企业每月处理的污水不低于1700吨,请你为该企业设计一种最省钱的购买方案.