备考2020年高考数学一轮复习:14 导数与函数的极值、最值
试卷更新日期:2019-09-03 类型:一轮复习
一、单选题
-
1. 函数 有( )A、最大值为1 B、最小值为1 C、最大值为 D、最小值为2. 函数 在 上的最大值为( )A、 B、 C、 D、3. 函数 在 上的最大值为( )A、 B、 C、 D、04. 函数 的极值点是( )A、 B、 C、 或-1或0 D、5. 设函数 在R上可导,其导函数为 ,且函数 的图像如图所示,则下列结论中一定成立的是( )
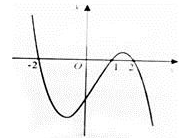 A、函数 有极大值 和极小值 B、函数 有极大值 和极小值 C、函数 有极大值 和极小值 D、函数 有极大值 和极小值6. 的最大值为( )A、1+ B、3 C、2+ D、47. 函数 , 的最大值是( )A、 B、 C、 D、8. 函数 , 的最大值是( )A、 B、 C、 D、9. 函数 ,已知 在 处取得极值,则 等于( )A、2 B、3 C、4 D、510. 若函数 在 上有最大值无最小值,则实数 的取值范围为( )A、 B、 C、 D、11. 函数 的极大值为 ,那么 的值是( )A、 B、 C、 D、12. 若函数 在 上的最大值为 ,则 =( )A、 B、 C、 D、
A、函数 有极大值 和极小值 B、函数 有极大值 和极小值 C、函数 有极大值 和极小值 D、函数 有极大值 和极小值6. 的最大值为( )A、1+ B、3 C、2+ D、47. 函数 , 的最大值是( )A、 B、 C、 D、8. 函数 , 的最大值是( )A、 B、 C、 D、9. 函数 ,已知 在 处取得极值,则 等于( )A、2 B、3 C、4 D、510. 若函数 在 上有最大值无最小值,则实数 的取值范围为( )A、 B、 C、 D、11. 函数 的极大值为 ,那么 的值是( )A、 B、 C、 D、12. 若函数 在 上的最大值为 ,则 =( )A、 B、 C、 D、二、填空题
-
13. 设函数f(x)=x3- x2-2x+5,若对任意x∈[1,2]都有f(x)<m成立,则实数m的取值范围是 .14. 已知函数 有两个极值点,则实数 的取值范围是 .15. 已知函数 的最小值为3,则 .16. 函数 在 时有极值10,那么 、 的值为.17. 函数 在 上的最大值是.
三、解答题