备考2020年高考数学一轮复习:13 导数与函数的单调性
试卷更新日期:2019-09-03 类型:一轮复习
一、单选题
-
1. 函数 的单调增区间是 ( )A、 B、 C、 D、2. 设 ,则此函数在区间 和 内分别( )A、单调递增,单调递减 B、单调递减,单调递增 C、单调递增,单调递增 D、单调递减,单调递减3. 函数 的单调递减区间为( )A、 B、 C、 D、4. 若函数 在区间 单调递增,则 的取值范围是( )A、 B、 C、 D、5. 函数 的单调递减区间是( )A、 B、 C、 D、6. 函数 在 上单调递增,则实数 的取值范围为( )A、 B、 C、 D、7. 函数 的递减区间为( )A、 B、 C、 D、8. 已知函数 满足 ,则 的单调递增区间为A、 B、 C、 D、9. 函数 是减函数的区间为( )A、 B、 C、 D、10. 函数 在区间 内是增函数,则实数 的取值范围是( )A、 B、 C、 D、11. 已知 在 上存在三个单调区间,则 的取值范围是( )A、 或 B、 C、 D、 或12. 函数 在区间 , 内是增函数, 则实数 的取值范围是A、
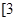 ,
,  B、
B、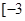 ,
,  C、
C、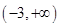 D、
D、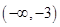
二、填空题
-
13. 已知函数 在 上单调递增,则实数 的取值范围是14. 函数 的最小值为 .15. 已知函数 上任一点 处的切线斜率 则该函数的单调递增区间为.