备考2020年高考数学一轮复习:12 变化率与导数、导数的计算
试卷更新日期:2019-09-03 类型:一轮复习
一、单选题
-
1. 曲线y=2sinx+cosx在点(π,-1)处的切线方程为 ( )A、x-y-π-1=0 B、2x-y-2π-1=0 C、2x+y-2π+1=0 D、x+y-π+1=02. 下列求导运算的正确是( )A、 为常数 B、 C、 D、3. 已知曲线 的一条切线的斜率为2,则切点的横坐标为( )A、1 B、ln2 C、2 D、e4. 一物体做直线运动,其位移 (单位: )与时间 (单位: )的关系是 ,则该物体在 时的瞬时速度是( )A、 B、 C、 D、5. 曲线 在点(1,1)处的切线方程为 =( )A、—4 B、—3 C、4 D、36. 若曲线 在点 处的切线的斜率为 ,则 ( )A、 B、 C、 D、7. 设函数 在 处存在导数,则 ( )A、 B、 C、 D、8. 设函数 的导函数为 ,且 ,则 =( )A、0 B、-4 C、-2 D、29. 函数 的导数为( )A、 =2 B、 = C、 =2 D、 =10. 下列求导运算正确的是( )A、 B、 C、 D、11. 给出定义:若函数 在D上可导,即 存在,且导函数 在D上也可导,则称 在D上存在二阶导函数,记 ,若 在D上恒成立,则称 在D上为凸函数。以下四个函数在 上不是凸函数的是( )A、 B、 C、 D、12. 如图所示,函数 y=f(x) 的图象在点P处的切线方程是 y=-x+5 ,则 =( )
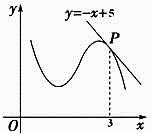 A、 B、1 C、2 D、0
A、 B、1 C、2 D、0二、填空题
-
13. 曲线y=3(x2+x)ex在点(0,0)处的切线方程为.14. 已知函数 的导函数为 ,若 ,则 的值为.15. 已知 ,则 .16. 已知函数 .若曲线 在点 处的切线方程为y=x,则a+b=.17. 已知函数 ,且函数 在点(2,f(2))处的切线的斜率是 ,则 =
三、解答题