备考2020年高考数学一轮复习:10 函数的图象
试卷更新日期:2019-09-03 类型:一轮复习
一、单选题
-
1. 在同一直角坐标系中,函数y= ,y=loga(x+ ),(a>0且a≠1)的图像可能是( )A、
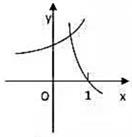 B、
B、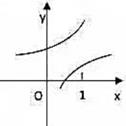 C、
C、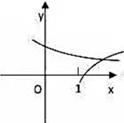 D、
D、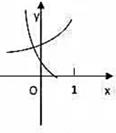 2. 函数 的图象可能是( )A、
2. 函数 的图象可能是( )A、 B、
B、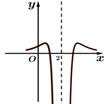 C、
C、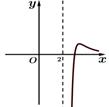 D、
D、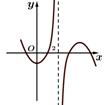 3. 已知函数f(x)图象如图所示,则该图象所对应的函数是( )
3. 已知函数f(x)图象如图所示,则该图象所对应的函数是( )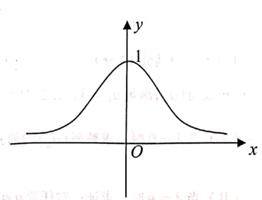 A、f(x)=e-x B、f(x)=e-2 C、f(x)=ex2 D、f(x)=e-x24. 函数 的图象大致为( )A、
A、f(x)=e-x B、f(x)=e-2 C、f(x)=ex2 D、f(x)=e-x24. 函数 的图象大致为( )A、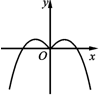 B、
B、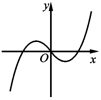 C、
C、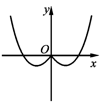 D、
D、 5. 函数 的图象大致为( )A、
5. 函数 的图象大致为( )A、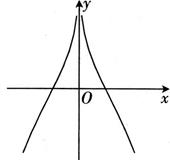 B、
B、 C、
C、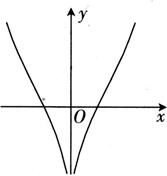 D、
D、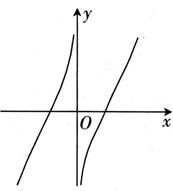 6. 函数 的图象大致为 ( )A、
6. 函数 的图象大致为 ( )A、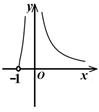 B、
B、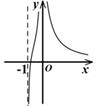 C、
C、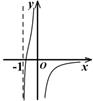 D、
D、 7. 函数 的图像可能是( )A、
7. 函数 的图像可能是( )A、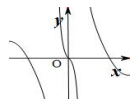 B、
B、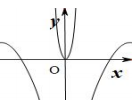 C、
C、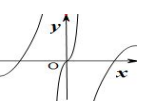 D、
D、 8. 函数 的图象是图中的A、
8. 函数 的图象是图中的A、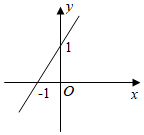 B、
B、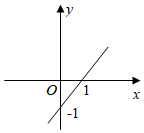 C、
C、 D、
D、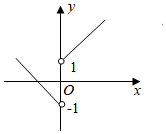 9. 函数 的图像大致为 ( )A、
9. 函数 的图像大致为 ( )A、 B、
B、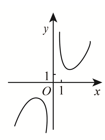 C、
C、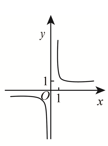 D、
D、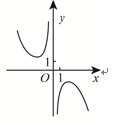 10. 函数 的图象可能是( )A、
10. 函数 的图象可能是( )A、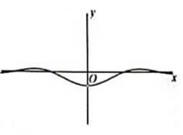 B、
B、 C、
C、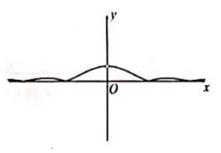 D、
D、 11. 下列函数中,其图像既是中心对称图形又在区间 上单调递增的是( )A、
11. 下列函数中,其图像既是中心对称图形又在区间 上单调递增的是( )A、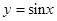 B、
B、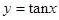 C、
C、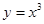 D、
D、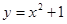 12. 已知函数 图象相邻两条对称轴的距离为 ,将函数 的图象向左平移 个单位后,得到的图象关于y轴对称则函数 的图象( )A、关于直线
12. 已知函数 图象相邻两条对称轴的距离为 ,将函数 的图象向左平移 个单位后,得到的图象关于y轴对称则函数 的图象( )A、关于直线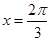 对称
B、关于直线
对称
B、关于直线  对称
C、关于点
对称
C、关于点 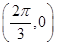 对称
D、关于点
对称
D、关于点 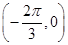 对称
对称
二、填空题
-
13. 已知 ,若 的图像和 的图像有四个不同的公共点,则实数 的取值范围是 .14. 若函数 与函数 的图象有且只有一个公共点,则 a 的取值范围是 .
15. 已知函数 的图象与 轴恰有2个不同的交点,则实数 的取值范围是 .16. 已知函数 f(x) 是 上的增函数, , 是其图象上的两点,则不等式 的解集是 .
17. 函数 的图象可能是下面的图象 填序号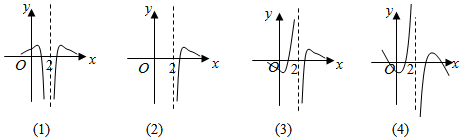
三、解答题
-
18. 已知函数 .
 (1)、在给出的坐标系中作出 的图象;(2)、根据图象,写出 的增区间;(3)、试讨论方程 的根的情况.19. 已知函数 .(1)、作出函数 的图象;(2)、若函数 的图象与函数 ( 为实数)的图象有两个交点,求实数 的取值范围.20. 已知函数 是定义在 上的偶函数,当 时, ( 为自然对数的底数).
(1)、在给出的坐标系中作出 的图象;(2)、根据图象,写出 的增区间;(3)、试讨论方程 的根的情况.19. 已知函数 .(1)、作出函数 的图象;(2)、若函数 的图象与函数 ( 为实数)的图象有两个交点,求实数 的取值范围.20. 已知函数 是定义在 上的偶函数,当 时, ( 为自然对数的底数). (1)、求函数 在 上的解析式,并作出 的大致图像;(2)、根据图像写出函数 的单调区间和值域.
(1)、求函数 在 上的解析式,并作出 的大致图像;(2)、根据图像写出函数 的单调区间和值域.