备考2020年高考数学一轮复习:09 对数函数
试卷更新日期:2019-09-02 类型:一轮复习
一、单选题
-
1. 设 , , ,则下列正确的是( )A、 B、 C、 D、2. 函数f(x)=loga(4-x)(a>0,且a≠1)的定义域是( )A、(0,4) B、(4,+∞) C、(-∞,4) D、(-∞,4)∪(4,+∞)3. 在同一直角坐标系中,函数 , 的图象可能是( )A、
 B、
B、 C、
C、 D、
D、 4. 设 ,则a,b,c 的大小是( )A、a>c>b B、b>a>c C、b>c>a D、a>b>c5. 若 ,则 的取值范围是( )A、 B、 C、 D、6. 设 , ,当 取最小值时 的值为( )A、2 B、3 C、4 D、57. 函数 的图象可能是( )A、
4. 设 ,则a,b,c 的大小是( )A、a>c>b B、b>a>c C、b>c>a D、a>b>c5. 若 ,则 的取值范围是( )A、 B、 C、 D、6. 设 , ,当 取最小值时 的值为( )A、2 B、3 C、4 D、57. 函数 的图象可能是( )A、 B、
B、 C、
C、 D、
D、 8. 以下运算正确的是( )A、 B、 C、 D、9. 设 , ,则 ( )A、
8. 以下运算正确的是( )A、 B、 C、 D、9. 设 , ,则 ( )A、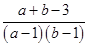 B、
B、 C、
C、 D、
D、 10. 函数y=lgx-1的零点是( )A、0 B、1 C、10 D、(10,0)11. 已知函数 在 上单调递减,且 , , ,则 的大小关系为( )A、
10. 函数y=lgx-1的零点是( )A、0 B、1 C、10 D、(10,0)11. 已知函数 在 上单调递减,且 , , ,则 的大小关系为( )A、 B、
B、 C、
C、 D、
D、 12. 已知 , , ,则 的大小关系为( )A、
12. 已知 , , ,则 的大小关系为( )A、 B、
B、 C、
C、 D、
D、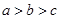
二、填空题
-
13. 若 ,则 ; .14. 已知x>0,y>0,且x+y=6,则 的最大值为15. 已知函数 的图象过定点 ,若点 也在函数 的图象上,则 .16. 已知实数 且 若 ,则 ;若 ,则实数 的取值范围是17. 16/17世纪之交,随着天文、航海、工程、贸易以及军事的发展,改进数字计算方法成了当务之急,约翰 纳皮尔正是在研究天文学的过程中,为了简化其中的计算而发明了对数.后来天才数学家欧拉发现了对数与指数的关系,即 .
现在已知 , ,则 .
18. 设任意实数 ,要使 恒成立,则 的最小值为 .三、解答题