备考2020年高考数学一轮复习:08 指数函数
试卷更新日期:2019-09-02 类型:一轮复习
一、单选题
-
1. 设 ,则 的大小关系为( )A、 B、 C、 D、2. 若a>0,且a≠1,则函数y=ax-1+1的图像一定过定点( )A、(0,1) B、(1,1) C、(1,2) D、(0,-1)3. 已知函数 , ,则 ( )A、1 B、
 C、
D、
C、
D、 4. 函数 的图象大致为( )A、
4. 函数 的图象大致为( )A、 B、
B、 C、
C、 D、
D、 5. 如果 ,那么( )A、
5. 如果 ,那么( )A、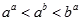 B、
B、 C、
C、 D、
D、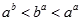 6. 函数 在[1,2]上的最大值比最小值大 ,则 =( )A、 B、 C、 或 D、 或7. 已知函数 ,则函数y=f(x+1)的图象大致是( )A、
6. 函数 在[1,2]上的最大值比最小值大 ,则 =( )A、 B、 C、 或 D、 或7. 已知函数 ,则函数y=f(x+1)的图象大致是( )A、 B、
B、 C、
C、 D、
D、 8. 若函数f(x)=a|x+1|(a>0.a≠1)的值域为[1,+∞),则f(-4)与f(0)的关系是( )A、
8. 若函数f(x)=a|x+1|(a>0.a≠1)的值域为[1,+∞),则f(-4)与f(0)的关系是( )A、 B、
B、 C、
C、 D、不能确定
9. 函数 在 上的最大值与最小值的和为 ,则 ( )A、2 B、3 C、
D、不能确定
9. 函数 在 上的最大值与最小值的和为 ,则 ( )A、2 B、3 C、 D、
10. 若函数 ( ,且 )的图象经过第二、三、四象限,则一定有( )A、 且 B、 且 C、 且 D、 且11. 函数 的值域是( )A、 B、 C、 D、12. 函数 ,且 的图象过一个定点,则这个定点坐标是( )A、
D、
10. 若函数 ( ,且 )的图象经过第二、三、四象限,则一定有( )A、 且 B、 且 C、 且 D、 且11. 函数 的值域是( )A、 B、 C、 D、12. 函数 ,且 的图象过一个定点,则这个定点坐标是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 对不同的 且 ,函数 必过一个定点 ,则点 的坐标是.14. 设函数 的图象与 的图象关于直线 对称,且 ,则实数 .15. 函数 在 上的值域为 .16. 以下是三个变量y1 , y2 , y3随变量x变化的函数值表:
x
1
2
3
4
5
6
7
8
…
y1
2
4
8
16
32
64
128
256
…
y2
1
4
9
16
25
36
49
64
…
y3
0
1
1.585
2
2.322
2.585
2.807
3
…
其中,关于x呈指数函数变化的函数是 .
17. 若指数函数f(x)=ax(a>0,且a≠1)的图象经过点(3,8),则f(-1)的值为三、解答题
-
18. 已知 ( ).(1)、当 ,且 的解集为 ,求函数 的解析式;(2)、若关于x的不等式 对一切实数恒成立,求实数 的取值范围.19. 求不等式 中 的取值范围。