福建省三明市大田县2018-2019学年八年级上学期数学期中考试试卷

试卷更新日期：2019-09-02 类型：期中考试

进入出卷网下载

一、单选题

1. 在实数5， $\frac{22}{7}$ ， $\sqrt{3}$ ， $\sqrt{4}$ 中，无理数是 $($ $)$

A、5 B、 $\frac{22}{7}$ C、 $\sqrt{3}$ D、 $\sqrt{4}$

查看试题解析
2. 在下列所给出坐标的点中，在第二象限的是（）

A、（2，3） B、（﹣2，3） C、（﹣2，﹣3） D、（2，﹣3）

查看试题解析
3. 下列各组数据中，不是勾股数的是 $($ $)$

A、3，4，5 B、7，24，25 C、8，15，17 D、5，7，9

查看试题解析
4. 如图，有一羽毛球场地是长方形，如果 $AB = 8$ 米， $AD = 6$ 米，若你要从A走到C，至少走 $($ $)$

A、14米 B、12米 C、10米 D、9米

查看试题解析
5. 如图，是用围棋子摆出的图案，围棋子的位置用有序数对表示，如：A点在（5，1），若再摆放一枚黑棋子，要使8枚棋子组成的图案是轴对称图形，则下列摆放错误的是（）

A、黑（2，3） B、黑（3，2） C、黑（3，4） D、黑（3，1）

查看试题解析
6. 如图，射线l是下列哪个函数的图象 $($ $)$

A、 $y = \frac{x^{2}}{x}$ B、 $y = {(\sqrt{x})}^{2}$ C、 $y = 5 x - 4 x$ D、 $y = | x |$

查看试题解析
7. 一次函数 $y_{1} = - x + b$ 的图象与 $y_{2} = x + 4$ 的图象的交点不可能在 $($ $)$

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 无理数 $- \sqrt{7}$ 在数轴上表示时的大概位置是（）

A、E点 B、F点 C、G点 D、H点

查看试题解析
9. 已知一次函数y=kx+3（k≠0）的图象经过点A，且函数值y随x的增大而增大，则点A的坐标可能是（）

A、（﹣2，﹣4） B、（1，2） C、（﹣2，4） D、（2，﹣1）

查看试题解析
10. 如图，在三角形纸片ABC中， $∠ A = 90^{\circ}$ ， $AB = 12$ ， $AC = 5$ 折叠三角形纸片，使点A在BC边上的点E处，则AD是 $($ $)$

A、3 B、4 C、 $\frac{10}{3}$ D、 $\frac{11}{3}$

查看试题解析

二、填空题

11. 点 $A (- 3, 4)$ 关于y轴对称的坐标为．

查看试题解析
12. 已知点 $P_{1} (- 2, y_{1})$ ， $P_{2} (- 1, y_{2})$ 是一次函数 $y = - 5 x + b$ 图象上的两个点，则 $y_{1}$ $y_{2}$ （填“＞”或“＜”“＝”）

查看试题解析
13. 如图，我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形，若小正方形与大正方形的面积之比为1：13，则直角三角形较短的直角边a与较长的直角边b的比值为．

查看试题解析
14. 如图，数轴上点A，B分别对应1，2，过点B作PQ⊥AB，以点B为圆心，AB长为半径画弧，交PQ于点C，以原点O为圆心，OC长为半径画弧，交数轴于点M，则点M对应的数是。

查看试题解析
15. 如图，已知a，b，c分别是Rt△ABC的三条边长，∠C=90°，我们把关于x的形如y= $\frac{a}{c} x + \frac{b}{c}$ 的一次函数称为“勾股一次函数”，若点P（1， $\frac{3 \sqrt{5}}{5}$ ）在“勾股一次函数”的图象上，且Rt△ABC的面积是5，则c的值是．

查看试题解析

三、解答题

16.

(1)、 $\sqrt{3} \times \sqrt{12} - \sqrt{25}$

(2)、 $(\sqrt{2} - \sqrt{3}) + \sqrt{18} \div \sqrt{3}$

查看试题解析
17. 根据题意，解答问题：

(1)、如图 $①$ ，已知直线 $y = 2 x + 4$ 与x轴、y轴分别交于A、B两点，求线段AB的长．

(2)、如图 $②$ ，类比 $(1)$ 的解题过程，请你通过构造直角三角形的方法，求出点 $M (3 ， 4)$ 与点 $N (- 2 ， - 1)$ 之间的距离．

查看试题解析
18. 先阅读，再解答
由 $(\sqrt{5} + \sqrt{3}) (\sqrt{5} - \sqrt{3}) = {(\sqrt{5})}^{2} - {(\sqrt{3})}^{2} = 2$ 可以看出，两个含有二次根式的代数式相乘，积不含有二次根式，我们称这两个代数式互为有理化因式，在进行二次根式计算时，利用有理化因式，有时可以化去分母中的根号，例如： $\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$ ，请完成下列问题：

(1)、求 $\sqrt{2}$ -1的有理化因式；

(2)、化去式子分母中的根号： $\frac{2}{3 \sqrt{2}}$ ， $\frac{3}{3 - \sqrt{6}}$ ；

(3)、比较 $\sqrt{2019} - \sqrt{2018}$ 与 $\sqrt{2018} - \sqrt{2017}$ 的大小，并说明理由．

查看试题解析
19. 如图，已知火车站的坐标为 $(2 ， 2)$ ，文化宫的坐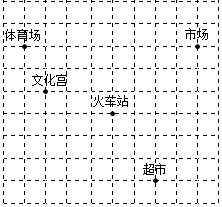标为 $(- 1 ， 3)$ ．

(1)、请你根据题目条件，画出平面直角坐标系；

(2)、写出体育场、市场、超市的坐标；

查看试题解析
20. 一如图，已知四边形ABCD中， $AB = 3$ ， $AD = 4$ ， $BC = 13$ ， $CD = 12$ ，且 $∠ A = 90^{\circ}$ ，连接BD，试判断 $△ BDC$ 的形状，并说明理由．

查看试题解析
21. 某数学兴趣小组根据学习一次函数的经验，对函数y=|x﹣1|的图象与性质进行了探究，下面是该小组的探究过程，请补充完整：

(1)、列表：

x

…

﹣1

0

1

2

3

…

y

…

b

1

0

1

2

…

其中，b=；

(2)、描点并连线：画出该函数的图象；

(3)、根据图象直接写出一个正确的结论．

查看试题解析
22. 对于实数p，q，我们用符号 $max {p ， q}$ 引表示p，q两数中较大的数，如： $max {1 ， 2} = 2$ ，

(1)、请直接写出； $max {- \sqrt{3} ， - \sqrt{5}}$ ；

(2)、我们知道，当 $m^{2} = 1$ 时， $m = \pm 1$ ，利用这种方法解决下面问题：若 $max {{(x - 1)}^{2} ， x^{2}} = 4$ ，其中 $(x < \frac{1}{2})$ ，求x的值．

查看试题解析
23. 如图

(1)、如图①是一个重要公式的几何解释．请你写出这个公式；

(2)、如图②，Rt△ABC≌Rt△CDE，∠B＝∠D＝90°，且B、C、D三点在一条直线上．试证明∠ACE＝90°；

(3)、伽菲尔德(G a rfield，1881年任美国第20届总统)利用（1）中的公式和图②证明了勾股定理(1876年4月1日，发表在《新英格兰教育日志》上)，现请你尝试该证明过程．

查看试题解析
24. 如图，在平面直角坐标系中，过点A（0，6）的直线AB与直线OC相交于点C（2，4）动点P沿路线O→C→B运动．

(1)、求直线AB的解析式；

(2)、当△OPB的面积是△OBC的面积的 $\frac{1}{4}$ 时，求出这时点P的坐标；

(3)、是否存在点P，使△OBP是直角三角形？若存在，直接写出点P的坐标，若不存在，请说明理由．

查看试题解析

x	…	﹣1	0	1	2	3	…
y	…	b	1	0	1	2	…