福建省晋江市安海片区2018-2019学年八年级上学期数学期中考试试卷

试卷更新日期：2019-09-02 类型：期中考试

进入出卷网下载

一、单选题

1. 下列说法正确的是（）

A、9的算术平方根是3 B、4的平方根是2 C、-3的平方根是 $\sqrt{- 3}$ D、8的立方根是±2

查看试题解析
2. 在实数|﹣3|，﹣ $\sqrt{2}$ ，0，-π中，最小的数是（）

A、|﹣3| B、﹣ $\sqrt{2}$ C、0 D、-π

查看试题解析
3. 下列计算中，正确的是（）

A、a²•a⁴=a⁸ B、（a³）²=a⁵ C、（3ax）²=9a²x² D、a²+a²=a⁴

查看试题解析
4. 下列从左边到右边的变形，属于因式分解的是（）

A、(x+1)(x-1)=x²-1 B、x²-2x+1=x(x-2)+1 C、x²-4y²=(x-2y)² D、2x²+4x+2=2(x+1)²

查看试题解析
5. 如图，在公园长方形空地上，要修两条路（图中的阴影所示），按照图中标的数据，计算图中空白部分的面积为（）

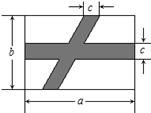A、ab-bc-ac+c² B、bc-ab+ac C、b²-bc+a²-ab D、a²+ab+bc-ac

查看试题解析
6. 若把代数式x²-2x+3化为(x-m)²+k的形式，其中m，k为常数，结果正确的是（）

A、(x+1)²+4 B、(x-1)²+2 C、(x-1)²+4 D、(x+1)²+2

查看试题解析
7. 下列选项，能说明命题“任何偶数都是8的整数倍”是假命题的反例是（）

A、2k（k为常数） B、15 C、24 D、42

查看试题解析
8. 如图， $A B = A D$ ，∠1＝∠2，则不一定能使△ABC≌△ADE的条件是（）

A、∠B＝∠D B、∠C=∠E C、BC＝DE D、AC＝AE

查看试题解析
9. 如图所示，在边长为a的正方形中，剪去一个边长为b的小正方形(a＞b)，将余下部分拼成一个梯形，根据两个图形阴影部分面积的关系，可以得到一个关于a、b的恒等式为（）

A、 ${(a - b)}^{2} = a^{2} - 2 ab + b^{2}$ B、 ${(a + b)}^{2} = a^{2} + 2 ab + b^{2}$ C、 $a^{2} - b^{2} = (a + b) (a - b)$ D、 $a^{2} + ab = a (a + b)$

查看试题解析
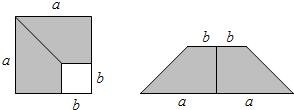10. 如图，两个正方形的边长分别为a，b，如果a+b=ab=9，则阴影部分的面积为（）

A、9 B、18 C、27 D、36

查看试题解析

二、填空题

11. 我们知道 $\sqrt{5}$ 是一个无理数，那么 $\sqrt{5}$ －1的整数部分是

查看试题解析
12. 如果 $\sqrt{x - 2}$ +(2y+1)²=0，那么x²⁰¹⁸y²⁰¹⁷=

查看试题解析
13. 已知m²﹣n²＝16，m+n＝6，则m﹣n＝．

查看试题解析
14. 如图，∠ACB＝90°，AC＝BC，BE⊥CE，AD⊥CE，垂足分别为E，D，AD＝25，DE＝17，则BE＝．

查看试题解析
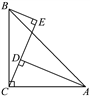15. 如图，C是△ABE的BE边上一点，F在AE上，D是BC的中点，且AB＝AC＝CE，对于下列结论：①AD⊥BC；②CF⊥AE；③∠1＝∠2；④AB＋BD＝DE.其中正确的结论有(填序号)．

查看试题解析
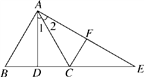16. 已知a-b=4，(a-3)(b+4)<ab

(1)、b的取值范围是

(2)、若a²+a+2ab-b+b²=40，则a的值是

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt[3]{64}$ - $\sqrt{{(- 2)}^{2}}$ +|2- $\sqrt{5}$ |

(2)、(a+2b)(a-2b)+(9a²b³-6a⁴b)÷(-3a²b)

查看试题解析
18. 分解因式：(x+2)(x-6)+16

查看试题解析
19. 先化简，再求值：
（x﹣2y）²﹣x（x+3y）﹣4y² ，其中x=﹣4，y= $\frac{1}{2}$ ．

查看试题解析
20. 已知 $A = \sqrt[a - b]{a + b + 36}$ 是a＋b＋36的算术平方根，B＝a－2b是27的立方根，求：A＋B的平方根．

查看试题解析
21.

(1)、请用“＞”、“＜”、“=”填空：
①3²+2²2×3×2； ② 5²+5²2×5×5；

③（-2）²+（-2）²2×（-2）×（-2）

④4²+（-3）²2×4×（-3）

(2)、观察以上各式，请猜想a²+b²与2ab的大小；并借助完全平方公式证明你的猜想．

查看试题解析
22. 求证：全等三角形对应边上的中线相等（请根据图形，写出已知、求证、证明）

已知：

求证：

证明：

查看试题解析
23. 如图，长为60cm，宽为x（cm）的大长方形被分割为7小块，除阴影A、B外，
其余5块是形状、大小完全相同的小长方形，其较短一边长为y(cm)．

(1)、分别用含x，y的代数式表示阴影A，阴影B的面积，并计算阴影A与阴影B的面积差．

(2)、当y为何值时，阴影A与阴影B的面积差与x的取值无关.

查看试题解析
24. 如图，在长方形ABCD中，AB=4cm，BC=6cm，点E为AB中点，如果点P在线段BC上以每秒2cm的速度由点B向点C运动，同时，点Q在线段CD上由点C向点D运动．设运动时间为t秒.

(1)、当t=2时，求△EBP的面积

(2)、若点Q以与点P不同的速度运动，经过几秒△BPE与△CQP全等，此时点Q的速度是多少？

(3)、若点Q以(2)中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿长方形ABCD的四边运动，求经过多长时间点P与点Q第一次在长方形ABCD的哪条边上相遇？

查看试题解析
25. 如图

(1)、问题背景：如图1，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，E、F分别是BC，CD上的点，且∠EAF＝60°，探究图中线段BE，EF，FD之间的数量关系．小王同学探究此问题的方法是延长FD到点G，使DG＝BE，连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是；

(2)、探索延伸：如图2，若在四边形ABCD中，AB＝AD，∠B＋∠D＝180°，E，F分别是BC，CD上的点，且∠EAF＝ $\frac{1}{2}$ ∠BAD，上述结论是否仍然成立，并说明理由；

(3)、结论应用：如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等．接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进，1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇与指挥中心O之间夹角∠EOF=70°，试求此时两舰艇之间的距离．

查看试题解析