安徽省淮南市潘集区2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期:2019-09-02 类型:期中考试
一、单选题
-
1. 下列五个黑体汉字中,轴对称图形的有( )
 A、1个 B、2个 C、3个 D、4个2. 一个三角形的三边长分别为a,b,c,则a,b,c的值不可能是( )A、3,4,5 B、5,7,7 C、10,6,4.5 D、4,5,93. 在联欢会上,有A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的( )A、三边中线的交点 B、三条角平分线的交点 C、三边中垂线的交点 D、三边上高的交点4. 画∠AOB的角平分线的方法步骤是:
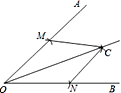
A、1个 B、2个 C、3个 D、4个2. 一个三角形的三边长分别为a,b,c,则a,b,c的值不可能是( )A、3,4,5 B、5,7,7 C、10,6,4.5 D、4,5,93. 在联欢会上,有A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的( )A、三边中线的交点 B、三条角平分线的交点 C、三边中垂线的交点 D、三边上高的交点4. 画∠AOB的角平分线的方法步骤是:①以O为圆心,适当长为半径作弧,交OA于M点,交OB于N点;②分别以M,N为圆心,大于 MN的长为半径作弧,两弧在∠AOB的内部相交于点C;③过点C作射线OC.射线OC就是∠AOB的角平分线.请你说明这样作角平分线的根据是( )
 A、SSS B、SAS C、ASA D、AAS5. 在△ABC和△DEF中,给出下列四组条件:
A、SSS B、SAS C、ASA D、AAS5. 在△ABC和△DEF中,给出下列四组条件:①AB=DE,BC=EF,AC=DF;
②AB=DE,∠B=∠E,BC=EF;
③∠B=∠E,BC=EF,AC=DF;
④∠A=∠D,∠B=∠E,∠C=∠F.
其中,能使△ABC≌△DEF的条件共有( )
A、1组 B、2组 C、3组 D、4组6. 设四边形的内角和等于a,六边形的外角和等于b,则a与b的关系是( )A、a>b B、a<b C、a=b D、b=a+360°7. 如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是( ) A、110° B、120° C、130° D、140°8. 如图,AB∥CD , BP和CP分别平分∠ABC和∠DCB , AD过点P , 且与AB垂直.若AD=8,则点P到BC的距离是( )
A、110° B、120° C、130° D、140°8. 如图,AB∥CD , BP和CP分别平分∠ABC和∠DCB , AD过点P , 且与AB垂直.若AD=8,则点P到BC的距离是( )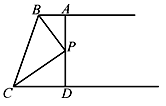 A、8 B、6 C、4 D、29. 如图,小明从A点出发,沿直线前进10米后向左转36°,再沿直线前进10米,再向左转36°……照这样走下去,他第一次回到出发点A点时,一共走的路程是( )
A、8 B、6 C、4 D、29. 如图,小明从A点出发,沿直线前进10米后向左转36°,再沿直线前进10米,再向左转36°……照这样走下去,他第一次回到出发点A点时,一共走的路程是( )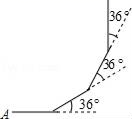 A、100米 B、110米 C、120米 D、200米10. 如图所示,在△ABC中,∠A=∠B=50°,AK=BN,AM=BK,则∠MKN的度数是( )
A、100米 B、110米 C、120米 D、200米10. 如图所示,在△ABC中,∠A=∠B=50°,AK=BN,AM=BK,则∠MKN的度数是( )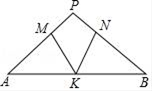 A、50° B、60° C、70° D、100°
A、50° B、60° C、70° D、100°二、填空题
-
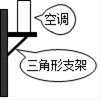
11. 空调安装在墙上时,一般都会采用如图所示的方法固定,这种方法应用的几何原理是.
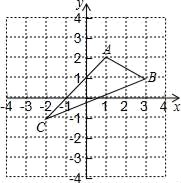
 12. 点P(1,-2)关于y轴对称的点P'的坐标为.
12. 点P(1,-2)关于y轴对称的点P'的坐标为.
13. 在镜子中看到时钟显示的是 ,则实际时间是 .
14. 如图,正方形ABCD中,截去∠A,∠C后,∠1,∠2,∠3,∠4的和为 .
,则实际时间是 .
14. 如图,正方形ABCD中,截去∠A,∠C后,∠1,∠2,∠3,∠4的和为 .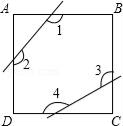 15. 如图,点B、F、C、E在一条直线上,已知BF=CE,AC∥DF,请你添加一个适当的条件 , 使得△ABC≌△DEF.
15. 如图,点B、F、C、E在一条直线上,已知BF=CE,AC∥DF,请你添加一个适当的条件 , 使得△ABC≌△DEF.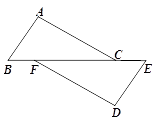 16. 如图,BP平分∠ABC,CP平分∠ACB,∠A=100°,则∠P= .
16. 如图,BP平分∠ABC,CP平分∠ACB,∠A=100°,则∠P= .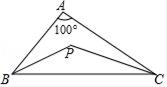 17. 如图,在△ABC中,DE是AC的垂直平分线,AE=4,△ABD的周长为14,则△ABC的周长为 .
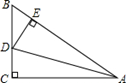
17. 如图,在△ABC中,DE是AC的垂直平分线,AE=4,△ABD的周长为14,则△ABC的周长为 . .18. 如图,在 ABC中,∠C=90°,AD平分∠BAC , DE⊥AB于E , 则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB; ④BE+AC=AB .
.18. 如图,在 ABC中,∠C=90°,AD平分∠BAC , DE⊥AB于E , 则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB; ④BE+AC=AB .一定成立的结论有(填序号).
三、解答题
-
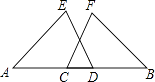
19. 如图,点A,C,D,B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF,求证:DE=CF.
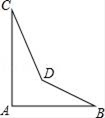
 20. 一个多边形的内角和是它的外角和的6倍,求这个多边形的边数.21. 某零件如图所示,按规定∠A=90°,∠B=32°,∠C=21°,当检验员量得∠BDC=146°,就断定这个零件不合格,你能说出其中的道理吗?
20. 一个多边形的内角和是它的外角和的6倍,求这个多边形的边数.21. 某零件如图所示,按规定∠A=90°,∠B=32°,∠C=21°,当检验员量得∠BDC=146°,就断定这个零件不合格,你能说出其中的道理吗?