福建省龙岩市上杭县2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2019-09-02 类型:期中考试
一、单选题
-
1. 下列手机手势解锁图案中,是中心对称图形的是A、
 B、
B、 C、
C、 D、
D、 2. 下列关于x的方程是一元二次方程的是A、 B、 C、 D、3. 用配方法解方程:x2﹣4x+2=0,下列配方正确的是( )A、(x﹣2)2=2 B、(x+2)2=2 C、(x﹣2)2=﹣2 D、(x﹣2)2=64. 方程 的解是(A、 B、 , C、 , D、 ,5. 抛物线y=(x+2)2﹣3可以由抛物线y=x2平移得到,则下列平移过程正确的是( )A、先向左平移2个单位,再向上平移3个单位 B、先向左平移2个单位,再向下平移3个单位 C、先向右平移2个单位,再向下平移3个单位 D、先向右平移2个单位,再向上平移3个单位6. 如图,将 绕点A按顺时针旋转一定角度得到 ,点B的对应点D恰好落在BC边上 若 , ,则CD的长为
2. 下列关于x的方程是一元二次方程的是A、 B、 C、 D、3. 用配方法解方程:x2﹣4x+2=0,下列配方正确的是( )A、(x﹣2)2=2 B、(x+2)2=2 C、(x﹣2)2=﹣2 D、(x﹣2)2=64. 方程 的解是(A、 B、 , C、 , D、 ,5. 抛物线y=(x+2)2﹣3可以由抛物线y=x2平移得到,则下列平移过程正确的是( )A、先向左平移2个单位,再向上平移3个单位 B、先向左平移2个单位,再向下平移3个单位 C、先向右平移2个单位,再向下平移3个单位 D、先向右平移2个单位,再向上平移3个单位6. 如图,将 绕点A按顺时针旋转一定角度得到 ,点B的对应点D恰好落在BC边上 若 , ,则CD的长为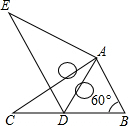 A、 B、 C、 D、17. 我县九州村某梨园2016年产量为1000吨,2018年产量为1440吨,求该梨园梨产量的年平均增长率,设该梨园梨产量的年平均增长量为x , 则根据题意可列方程为A、1440(1-x)2= 1000 B、1440(1+x)2= 1000 C、1000(1-x)2= 1440 D、1000(1+x)2= 14408. 已知二次函数 的图象与x轴的一个交点为 ,则关于x的方程 的两实数根分别是A、1和 B、1和 C、1和2 D、1和39. 若函数 的图象与坐标轴有三个交点,则b的取值范围是
A、 B、 C、 D、17. 我县九州村某梨园2016年产量为1000吨,2018年产量为1440吨,求该梨园梨产量的年平均增长率,设该梨园梨产量的年平均增长量为x , 则根据题意可列方程为A、1440(1-x)2= 1000 B、1440(1+x)2= 1000 C、1000(1-x)2= 1440 D、1000(1+x)2= 14408. 已知二次函数 的图象与x轴的一个交点为 ,则关于x的方程 的两实数根分别是A、1和 B、1和 C、1和2 D、1和39. 若函数 的图象与坐标轴有三个交点,则b的取值范围是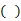 A、 且 B、 C、 D、10. 如图,点A , B的坐标分别为 和 ,抛物线y=a(x-m)2+n的顶点在线段AB上运动 抛物线随顶点一起平移 ,与x轴交于C、D两点 在D的左侧 ,点C的横坐标最小值为 ,则点D的横坐标最大值为
A、 且 B、 C、 D、10. 如图,点A , B的坐标分别为 和 ,抛物线y=a(x-m)2+n的顶点在线段AB上运动 抛物线随顶点一起平移 ,与x轴交于C、D两点 在D的左侧 ,点C的横坐标最小值为 ,则点D的横坐标最大值为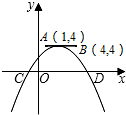 A、 B、1 C、5 D、8
A、 B、1 C、5 D、8二、填空题
-
11. 已知 是二次函数,则 .12. 菱形的两条对角线长分别是方程 的两实根,则菱形的面积为 .13. 已知m是关于x的方程 的一个根,则 = .14. 已知抛物线y=a(x+1)2 经过点 , ,则 填“ ”,“ ”,或“ ” .15. 如图,在平面直角坐标系中,点A在抛物线 上运动,过点A作 轴于点C , 以AC为对角线作矩形ABCD , 连接BD , 则对角线BD的最小值为 .
 16. 如图,二次函数 的图象与x轴交于A , B两点,与y轴交于点C , 且 ,则下列结论: ; ; ; 其中正确结论的序号是 .
16. 如图,二次函数 的图象与x轴交于A , B两点,与y轴交于点C , 且 ,则下列结论: ; ; ; 其中正确结论的序号是 .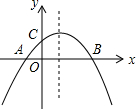
三、解答题
-
17. 某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)、求出y与x的函数关系式;
(2)、当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?(3)、设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
18. 解方程(1)、 ;(2)、 .19. 如图, 三个顶点的坐标分别为 , , .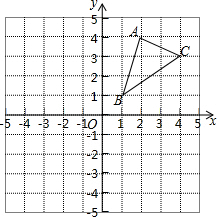 (1)、请画出 关于原点对称的 ,并写出 , , 的坐标;(2)、请画出 绕点B逆时针旋转 后的 .20. 观察下列一组方程: ; ; ; ; 它们的根有一定的规律,都是两个连续的自然数,我们称这类一元二次方程为“连根一元二次方程”.(1)、若 也是“连根一元二次方程”,写出k的值,并解这个一元二次方程;(2)、请写出第n个方程和它的根.21. 已知关于x的方程 ,求证:不论k取任何实数,该方程都有实数根.22. 已知抛物线的顶点为 ,与y轴交点为(1)、求该抛物线的解析式,并画出抛物线的草图 无需列表,要求标出抛物线与坐标轴的交点坐标 .(2)、观察图象,写出当 时,自变量x的取值范围.23. 参与两个数学活动,再回答问题:
(1)、请画出 关于原点对称的 ,并写出 , , 的坐标;(2)、请画出 绕点B逆时针旋转 后的 .20. 观察下列一组方程: ; ; ; ; 它们的根有一定的规律,都是两个连续的自然数,我们称这类一元二次方程为“连根一元二次方程”.(1)、若 也是“连根一元二次方程”,写出k的值,并解这个一元二次方程;(2)、请写出第n个方程和它的根.21. 已知关于x的方程 ,求证:不论k取任何实数,该方程都有实数根.22. 已知抛物线的顶点为 ,与y轴交点为(1)、求该抛物线的解析式,并画出抛物线的草图 无需列表,要求标出抛物线与坐标轴的交点坐标 .(2)、观察图象,写出当 时,自变量x的取值范围.23. 参与两个数学活动,再回答问题:活动 :观察下列两个两位数的积 两个乘数的十位上的数都是9,个位上的数的和等于 ,猜想其中哪个积最大?
, , , , , , , , .
活动 :观察下列两个三位数的积 两个乘数的百位上的数都是9,十位上的数与个位上的数组成的数的和等于 ,猜想其中哪个积最大?
, , , , , , .
(1)、分别写出在活动 、 中你所猜想的是哪个算式的积最大?(2)、对于活动 ,请用二次函数的知识证明你的猜想.24. 如图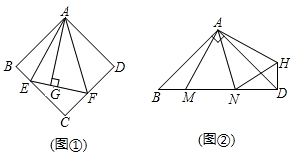 (1)、如图 ,在正方形ABCD中, 的顶点E , F分别在BC , CD边上,高AG与正方形的边长相等,求 的度数.(2)、如图 ,在 中, , ,点M , N是BD边上的任意两点,且 ,将 绕点A逆时针旋转 至 位置,连接NH , 试判断MN , ND , DH之间的数量关系,并说明理由.(3)、在图 中,连接BD分别交AE , AF于点M , N , 若 , , ,求AG , MN的长.25. 已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)、如图 ,在正方形ABCD中, 的顶点E , F分别在BC , CD边上,高AG与正方形的边长相等,求 的度数.(2)、如图 ,在 中, , ,点M , N是BD边上的任意两点,且 ,将 绕点A逆时针旋转 至 位置,连接NH , 试判断MN , ND , DH之间的数量关系,并说明理由.(3)、在图 中,连接BD分别交AE , AF于点M , N , 若 , , ,求AG , MN的长.25. 已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b. (1)、求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);(2)、直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;(3)、a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.
(1)、求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);(2)、直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;(3)、a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.