福建省龙岩市连城县2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2019-09-02 类型:期中考试
一、单选题
-
1. 方程x2﹣3=0的根是( )A、 B、﹣ C、± D、32. 将一元二次方程x2﹣4x﹣7=0配方,所得的方程是( )A、(x﹣2)2=11 B、(x﹣2)2=3 C、(x+2)2=11 D、(x+2)2=33. 一元二次方程2x2﹣5x﹣2=0的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根4. 抛物线y=2x2+4x﹣3的顶点坐标是( )A、(1,﹣5) B、(﹣1,﹣5) C、(﹣1,﹣4) D、(﹣2,﹣7)5. 满足函数y= x﹣1与y=﹣ 的图象为( )A、
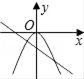 B、
B、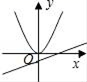 C、
C、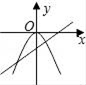 D、
D、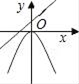 6. 下列所述图形中,既是轴对称图形又是中心对称图形的是( )A、等边三角形 B、平行四边形 C、正五边形 D、圆7. 过⊙O内一点P的最长弦长为10cm , 最短弦长为8cm , 那么OP的长为( )A、9 B、 C、6 D、38. 已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )A、2 cm B、4 cm C、2 cm或4 cm D、2 cm或4 cm9. 如图,AB是半圆的直径,点D是弧AC的中点,∠ABC=500 , 则∠DAB等于( )
6. 下列所述图形中,既是轴对称图形又是中心对称图形的是( )A、等边三角形 B、平行四边形 C、正五边形 D、圆7. 过⊙O内一点P的最长弦长为10cm , 最短弦长为8cm , 那么OP的长为( )A、9 B、 C、6 D、38. 已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )A、2 cm B、4 cm C、2 cm或4 cm D、2 cm或4 cm9. 如图,AB是半圆的直径,点D是弧AC的中点,∠ABC=500 , 则∠DAB等于( )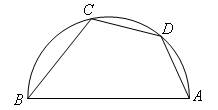 A、55° B、60° C、65° D、70°10. 要组织一次排球邀请赛,参赛的每个队之间要比赛两场,根据场地和时间等条件,赛程计划安排7天,每天安排8场比赛,若设比赛组织者应邀请x个队参赛,则x满足的关系式为( )A、 x(x+1)=56 B、 x(x﹣1)=56 C、x(x+1)=56 D、x(x﹣1)=56
A、55° B、60° C、65° D、70°10. 要组织一次排球邀请赛,参赛的每个队之间要比赛两场,根据场地和时间等条件,赛程计划安排7天,每天安排8场比赛,若设比赛组织者应邀请x个队参赛,则x满足的关系式为( )A、 x(x+1)=56 B、 x(x﹣1)=56 C、x(x+1)=56 D、x(x﹣1)=56二、填空题
-
11. 已知α,β是方程x2﹣3x﹣4=0的两个实数根,则α2+αβ﹣3α的值为 .
12. 若m是方程2x2﹣3x﹣1=0的一个根,则6m2﹣9m+2016的值为 .13. 已知直线y=x+2上有一点P(5,n),则点P关于原点的对称点P1的坐标为 .14. 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE , 点B的对应点D恰好落在BC边上,若AC= ,∠B=60°,则CD的长为 . 15. 如图,在边长为1的正方形网格中,若一段圆弧恰好经过四个格点,则该圆弧所在圆的圆心是图中的点 .
15. 如图,在边长为1的正方形网格中,若一段圆弧恰好经过四个格点,则该圆弧所在圆的圆心是图中的点 .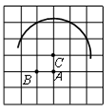 16. 平面直角坐标系下,一组有规律的点A1(0,1)、A2(1,0)、A3(2,1)、A4(3,0)、A5(4,1)、A6(5,0)…(注:当n为奇数时,An(n﹣1,1),n为偶数时,An(n﹣1,0)),抛物线C1经过点A1、A2、A3三点,…抛物线Cn经过Cn , Cn+1 , Cn+2三点,请写出抛物线C2n的解析式 .
16. 平面直角坐标系下,一组有规律的点A1(0,1)、A2(1,0)、A3(2,1)、A4(3,0)、A5(4,1)、A6(5,0)…(注:当n为奇数时,An(n﹣1,1),n为偶数时,An(n﹣1,0)),抛物线C1经过点A1、A2、A3三点,…抛物线Cn经过Cn , Cn+1 , Cn+2三点,请写出抛物线C2n的解析式 .三、解答题
-
17. 解关于x的一元二次方程:x2﹣2x=4.18. 已知抛物线y=ax2+bx﹣3(a≠0)经过点(﹣1,0),(3,0),求a,b的值.
19. 已知关于x的一元二次方程x2﹣(2m﹣2)x+(m2﹣2m)=0.(1)、求证:方程有两个不相等的实数根.
(2)、如果方程的两实数根为x1 , x2 , 且x12+x22=10,求m的值.
20. 如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.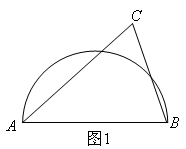
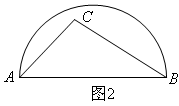 (1)、在图1中,画出△ABC的三条高的交点;(2)、在图2中,画出△ABC中AB边上的高.21. 如图,△ABC内接于⊙O , ∠BAC=120°,AB=AC , BD为⊙O的直径,AD=6,求弦DC的长.
(1)、在图1中,画出△ABC的三条高的交点;(2)、在图2中,画出△ABC中AB边上的高.21. 如图,△ABC内接于⊙O , ∠BAC=120°,AB=AC , BD为⊙O的直径,AD=6,求弦DC的长. 22. 阅读下面的例题:
22. 阅读下面的例题:例:解方程x2﹣2|x|﹣3=0
解:(1)当x≥0时,原方程可化为x2﹣2x﹣3=0,
解得x1=﹣1(舍去),x2=3;(2)当x<0时,原方程可化为x2+2x﹣3=0,解得x1=1(舍去),x2=﹣3.
综上所述,原方程的根是x1=3,x2=﹣3.
解答问题:
(1)、如果我们将原方程化为|x|2﹣2|x|﹣3=0求解可以吗?请你大胆试一下写出求解过程.(2)、依照题目给出的例题解法,解方程x2+2|x﹣2|﹣4=023. 某商场试销一种成本为60元/件的T恤,规定试销期间单价不低于成本单价,又获利不得高于40%,经试销发现,销售量y(件)与销售单价x(元/件)符合一次函数y=kx+b , 且x=70时,y=50;x=80时,y=40;(1)、求出一次函数y=kx+b的解析式(2)、若该商场获得利润为w元,试写出利润w与销售单价x之间的关系式,销售单价定为多少时,商场可获得最大利润,最大利润是多少?24. 如图 (1)、如图1,点P是等边△ABC内一点,已知PA=3,PB=4,PC=5,求∠APB的度数.
(1)、如图1,点P是等边△ABC内一点,已知PA=3,PB=4,PC=5,求∠APB的度数.要直接求∠A的度数显然很因难,注意到条件中的三边长恰好是一组勾股数,因此考虑借助旋转把这三边集中到一个三角形内,如图2,作∠PAD=60°使AD=AP , 连接PD , CD , 则△PAD是等边三角形.
∴=AD=AP=3,∠ADP=∠PAD=60°
∵△ABC是等边三角形
∴AC=AB , ∠BAC=60°
∴∠BAP=
∴△ABP≌△ACD
∴BP=CD=4,=∠ADC
∵在△PCD中,PD=3,PC=5,CD=4,PD2+CD2=PC2
∴∠PDC=°
∴∠APB=∠ADC=∠ADP+∠PDC=60°+90°=150°
(2)、如图3,在△ABC中,AB=BC , ∠ABC=90°,点P是△ABC内一点,PA=1,PB=2,PC=3,求∠APB的度数.25. 如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,C在x轴的正半轴上,已知A(0,8)、C(10,0),作∠AOC的平分线交AB于点D , 连接CD , 过点D作DE⊥CD交OA于点E .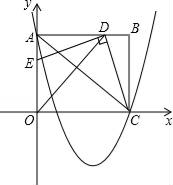 (1)、求点D的坐标;(2)、求证:△ADE≌△BCD;(3)、抛物线y= x2﹣ x+8经过点A、C , 连接AC . 探索:若点P是x轴下方抛物线上一动点,过点P作平行于y轴的直线交AC于点M . 是否存在点P , 使线段MP的长度有最大值?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求点D的坐标;(2)、求证:△ADE≌△BCD;(3)、抛物线y= x2﹣ x+8经过点A、C , 连接AC . 探索:若点P是x轴下方抛物线上一动点,过点P作平行于y轴的直线交AC于点M . 是否存在点P , 使线段MP的长度有最大值?若存在,求出点P的坐标;若不存在,请说明理由.