安徽省合肥市瑶海区2018-2019学年九年级上学期数学期中考试试卷

试卷更新日期：2019-09-02 类型：期中考试

进入出卷网下载

一、单选题

1. 下列函数是二次函数的是（）

A、 $y = - 3 x^{2} + π$ B、 $y = 2 x - 3$ C、 $y = 3 x^{2} + \frac{1}{x^{2}}$ D、 $y = a x^{2} + b x + c$

查看试题解析
2. 在平面直角坐标系中，抛物线 $y = x^{2} - 1$ 与 $x$ 轴的交点的个数是（）

A、3 B、2 C、1 D、0

查看试题解析
3. 在同一直角坐标系中，函数 $y = a x^{2} + b$ 与 $y = a x - b$ 的图像大致如图（）

A、 B、 C、 D、

查看试题解析
4. 已知 $\frac{a - b}{a} = \frac{3}{5}$ ，那么 $\frac{a}{b}$ 等于（）

A、 $\frac{2}{5}$ B、 $- \frac{5}{2}$ C、 $\frac{5}{2}$ D、 $- \frac{2}{5}$

查看试题解析
5. 已知点 $(- 1, y_{1}), (- 2, y_{2}), (3, y_{3})$ 在反比例函数 $y = \frac{- k^{2} - 1}{x}$ 的图像上，下列正确的是（）

A、 $y_{1} > y_{3} > y_{2}$ B、 $y_{1} > y_{2} > y_{3}$ C、 $y_{3} > y_{1} > y_{2}$ D、 $y_{3} > y_{2} > y_{1}$

查看试题解析
6. 如图中阴影部分的面积与函数 $y = - x^{2} + 2 x + \frac{1}{2}$ 的最大值相同的是（）

A、 B、 C、 D、

查看试题解析
7. 下列判断中唯一正确的是（）

A、函数 $y = a x^{2}$ 的图象开口向上，函数 $y = - a x^{2}$ 的图象开口向下 B、二次函数 $y = a x^{2}$ ，当 $x < 0$ 时， $y$ 随 $x$ 的增大而增大 C、 $y = 2 x^{2}$ 与 $y = - 2 x^{2}$ 图象的顶点、对称轴、开口方向、开口大小完全相同 D、抛物线 $y = a x^{2}$ 与 $y = - a x^{2}$ 的图象关于 $x$ 轴对称

查看试题解析
8. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，则下列结论：
① $a b c > 0 ；$ ② $2 a + b > 0 ；$ ③ $a - b + c < 0 ；$ ④ $4 a c - b^{2} < 0 ；$ ⑤ $b + a < 0 ，$ 其中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 若 $\frac{c}{a + b} = \frac{a}{b + c} = \frac{b}{a + c} = k$ ，则 $k$ 的值为（）

A、 $\frac{1}{2}$ B、 $1$ C、 $- 1$ D、 $\frac{1}{2} 或 - 1$

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x + c$ 中，当 $x = 0$ 时， $y = - 2$ ，且 $b$ 的平方等于 $a$ 与 $c$ 的乘积，则函数值有（）

A、最大值 $- 1.5$ B、最小值 $- 1.5$ C、最大值 $- 2.5$ D、最小值 $- 2.5$

查看试题解析

二、填空题

11. 把 $2$ 米长的线段进行黄金分割，则分成的较长的线段长为.

查看试题解析
12. 把抛物线 $y = a x^{2} + b x + c$ 先向右平移2个单位，再向下平移3个单位得到抛物线 $y = x^{2} - 2 x - 2$ ，那么原抛物线的解析式为．

查看试题解析
13. 在平面直角坐标系的第一象限内，边长为1的正方形 $A B C D$ 的边均平行于坐标轴， $A$ 点的坐标为 $(a ， a)$ .如图，若曲线 $y = \frac{4}{x} (x > 0)$ 与此正方形的边有交点，则 $a$ 的取值范围是.

查看试题解析
14. 已知二次函数 $y = - x^{2} - 2 x + 3$ ，当 $m \leq x \leq m + 3$ 时， $y$ 的取值范围是 $0 \leq y \leq 4$ ，则 $m$ 的值为．

查看试题解析

三、解答题

15. 已知抛物线 $y = x^{2} + b x + c$ 的图像经过点 $(0, 1)$ 和 $(1, 0)$ .求这个二次函数的关系式.

查看试题解析
16. 已知三个数2、4、8，请你再添上一个数，使它们成比例，求出所有符合条件的数．

查看试题解析
17. 抛物线 $y = - x^{2} + 4 x - 6$ .

(1)、请把二次函数写成 $y = a {(x + h)}^{2} + k$ 的形式；

(2)、 $x$ 取何值时， $y$ 随 $x$ 的增大而减小？

查看试题解析
18. 已知，矩形 $O A B C$ 中， $B C = 6$ ， $A B = 4$ ，它在平面直角坐标系中的位置如图所示，反比例函数 $y = \frac{k}{x} （ k \neq 0 ）$ 的图象经过矩形 $O A B C$ 对角线的交点 $D$ ．

(1)、试确定反比例函数的表达式；

(2)、若反比例函数 $y = \frac{k}{x} （ k \neq 0 ）$ 的图象与 $A B$ 交于点 $E$ ，求点 $E$ 的坐标．

查看试题解析
19. 如图，抛物线y= $\frac{1}{2}$ x²+bx﹣2与x轴交于A、B两点，与y轴交于C点，且A（﹣1，0）．

(1)、求抛物线的解析式；

(2)、判断△ABC的形状，证明你的结论．

查看试题解析
20. 合肥三十八中为预防秋季疾病传播，对教室进行“薰药消毒”．已知药物在燃烧释放过程中，室内空气中每立方米含药量 $y$ （毫克）与燃烧时间 $x$ （分钟）之间的关系如图所示（即图中线段 $O A$ 和双曲线在 $A$ 点及其右侧的部分），根据图象所示信息，解答下列问题：

(1)、写出从药物释放开始， $y$ 与 $x$ 之间的函数关系式及自变量的取值范围；

(2)、据测定，只有当空气中每立方米的含药量不低于 $5$ 毫克时，对预防才有作用，且至少持续作用 $20$ 分钟以上，才能完全杀死这种病毒，请问这次消毒是否彻底？

查看试题解析
21. 如图，一次函数y=kx+b与反比例函数y= $\frac{6}{x}$ （x＞0）的图象交于A（m，6），B（3，n）两点．

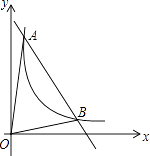(1)、求一次函数的解析式；

(2)、根据图象直接写出使kx+b＜ $\frac{6}{x}$ 成立的x的取值范围；

(3)、求△AOB的面积．

查看试题解析
22. 创新需要每个人的参与，就拿小华来说，为了解决晒衣服的，聪明的他想到了一个好办法，在家宽敞的院内地面 $(B D)$ 上立两根等长的立柱 $A B$ 、 $C D$ (均与地面垂直)，并在立柱之间悬挂一根绳子.由于挂的衣服比较多，绳子的形状近似成了抛物线 $y = a x^{2} - 0.8 x + c$ ，如图 $1$ ，已知立柱 $A B = C D = 2.6$ 米， $B D = 8$ 米.

(1)、求绳子最低点离地面的距离；

(2)、为了防止衣服碰到地面，小华在离 $A B$ 为 $3$ 米的位置处用一根垂直于地面的立柱 $M N$ 撑起绳子 (如图2)，使左边抛物线 $F_{1}$ 的最低点距 $M N$ 为 $1$ 米，离地面 $1.6$ 米，求 $M N$ 的长.

查看试题解析
23. 某旅游风景区出售一种纪念品，该纪念品的成本为12元/个，这种纪念品的销售价格为x（元/个）与每天的销售数量y（个）之间的函数关系如图所示．

(1)、求y与x之间的函数关系式；

(2)、销售价格定为多少时，每天可以获得最大利润？并求出最大利润．

(3)、“十•一”期间，游客数量大幅增加，若按八折促销该纪念品，预计每天的销售数量可增加200%，为获得最大利润，“十•一”假期该纪念品打八折后售价为多少？

查看试题解析