安徽省亳州市利辛县2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2019-09-02 类型:期中考试
一、单选题
-
1. 下列四条线段能成比例线段的是( )A、1,1,2,3 B、1,2,3,4 C、2,2,3,3 D、2,3,4,52. 已知A(x1 , y1)和B(x2 , y2)是反比例函数y= 的上的两个点,若x2>x1>0,则( )A、y2>y1>0 B、y1>y2>0 C、0>y1>y2 D、0>y2>y13. 抛物线y=3(x﹣2)2+5的顶点坐标是( )A、(﹣2,5) B、(﹣2,﹣5) C、(2,5) D、(2,﹣5)4. 下列各组中的四条线段成比例的是( )A、1cm、2cm、20cm、30cm B、1cm、2cm、3cm、4cm C、4cm、2cm、1cm、3cm D、5cm、10cm、10cm、20cm5. 当k取任意实数时,抛物线y=﹣9(x﹣k)2﹣3k2的顶点所在的曲线的解析式是( )
A、y=3x2 B、y=9x2 C、y=﹣3x2 D、y=﹣9x26. 如图,在同一平面直角坐标系中,一次函数y1=kx+b(k、b是常数,且k≠0)与反比例函数y2= (c是常数,且c≠0)的图象相交于A(﹣3,﹣2),B(2,3)两点,则不等式y1>y2的解集是( )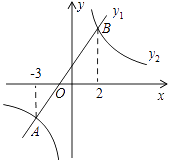 A、﹣3<x<2 B、x<﹣3或x>2 C、﹣3<x<0或x>2 D、0<x<27. 如图,点F是 ABCD的边AD上的三等分点,BF交AC于点E , 如果△AEF的面积为2,那么四边形CDFE的面积等于( )
A、﹣3<x<2 B、x<﹣3或x>2 C、﹣3<x<0或x>2 D、0<x<27. 如图,点F是 ABCD的边AD上的三等分点,BF交AC于点E , 如果△AEF的面积为2,那么四边形CDFE的面积等于( )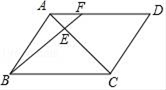 A、18 B、22 C、24 D、468. 当a≤x≤a+1时,函数y=x2-2x+1的最小值为1,则a的值为( )A、-1 B、2 C、0或2 D、-1或29. 已知二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+a与反比例函数y= 在同一平面直角坐标系中的图象大致是( )
A、18 B、22 C、24 D、468. 当a≤x≤a+1时,函数y=x2-2x+1的最小值为1,则a的值为( )A、-1 B、2 C、0或2 D、-1或29. 已知二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+a与反比例函数y= 在同一平面直角坐标系中的图象大致是( ) A、
A、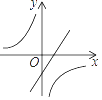 B、
B、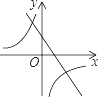 C、
C、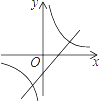 D、
D、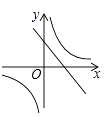 10. 已知:如图,点P是正方形ABCD的对角线AC上的一个动点(A、C除外),作PE⊥AB于点E,作PF⊥BC于点F,设正方形ABCD的边长为x,矩形PEBF的周长为y,在下列图象中,大致表示y与x之间的函数关系的是( )
10. 已知:如图,点P是正方形ABCD的对角线AC上的一个动点(A、C除外),作PE⊥AB于点E,作PF⊥BC于点F,设正方形ABCD的边长为x,矩形PEBF的周长为y,在下列图象中,大致表示y与x之间的函数关系的是( )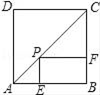 A、
A、 B、
B、 C、
C、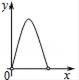 D、
D、
二、填空题
-
11. 已知线段a=4,b=1,如果线段c是线段a、b的比例中项,那么c= .12. 将二次函数y=x2﹣1的图象向上平移3个单位长度,得到的图象所对应的函数表达式是 .13. 在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是 .
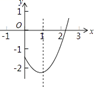 14. 两个三角形相似,相似比是 ,如果小三角形的面积是9,那么大三角形的面积是.15. 已知线段a、b、c满足 ,且 ,求 的值 .
14. 两个三角形相似,相似比是 ,如果小三角形的面积是9,那么大三角形的面积是.15. 已知线段a、b、c满足 ,且 ,求 的值 .三、解答题
-
16. 用配方法求二次函数y=x2﹣10x+3的顶点坐标.17. 如图,某测量工作人员眼睛A与标杆顶端F、电视塔顶端E在同一直线上,已知此人眼睛距地面1.6米,标杆高为3.2米,且BC=1米,CD=5米,求电视塔的高ED.
 18. 反比例函数 的图象经过点A (2,-3) .
18. 反比例函数 的图象经过点A (2,-3) .
(1)、求这个函数的解析式;(2)、请判断点B(1,6)是否在这个反比例函数的图象上,并说明理由.19. 由边长相等的小正方形组成的网格,以下各图中点A、B、C、D都在格点上.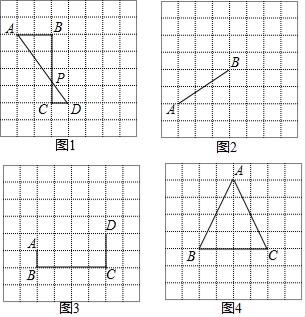 (1)、在图1中,PC:PB=;(2)、利用网格和无刻度的直尺作图,保留痕迹,不写作法.
(1)、在图1中,PC:PB=;(2)、利用网格和无刻度的直尺作图,保留痕迹,不写作法.①如图2,在AB上找点P,使得AP:PB=1:3;
②如图3,在BC上找点P,使得△APB∽△DPC;
③如图4,在△ABC中内找一点P,连接PA、P
B、PC,将△ABC分成面积相等的三部分.
20. 已知抛物线y=x2﹣(m+1)x+m(1)、求证:抛物线与x轴一定有交点;(2)、若抛物线与x轴交于A(x1 , 0),B(x2 , 0)两点,x1<0<x2 , 且 ,求m的值.21. 如图,四边形OP1A1B1、A1P2A2B2、A2P3A3B3、……、An-1PnAnBn都是正方形,对角线OA1、A1A2、A2A3、……、An-1An都在y轴上(n≥2),点P1(x1 , y1),点P2(x2 , y2),……,点Pn(xn , yn)在反比例函数y= (x>0)的图象上,已知B1 (-1,1)。 (1)、反比例函数解析式为;(2)、求点P1和点P2的坐标;(3)、点Pn的坐标为()(用含n的式子表示),△PnBnO的面积为。(直接填答案)22. 某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)、反比例函数解析式为;(2)、求点P1和点P2的坐标;(3)、点Pn的坐标为()(用含n的式子表示),△PnBnO的面积为。(直接填答案)22. 某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)、若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)、当降价多少元时,每星期的利润最大?最大利润是多少?23. 如图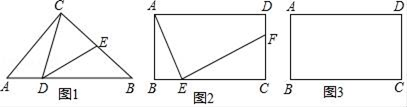 (1)、如图1所示,在Rt△ABC中,∠ACB=90°,AC=BC,点D在斜边AB上,点E在直角边BC上,若∠CDE=45°,求证:△ACD∽△BDE.(2)、如图2所示,在矩形ABCD中,AB=4cm,BC=10cm,点E在BC上,连接AE,过点E作EF⊥AE交CD(或CD的延长线)于点F.
(1)、如图1所示,在Rt△ABC中,∠ACB=90°,AC=BC,点D在斜边AB上,点E在直角边BC上,若∠CDE=45°,求证:△ACD∽△BDE.(2)、如图2所示,在矩形ABCD中,AB=4cm,BC=10cm,点E在BC上,连接AE,过点E作EF⊥AE交CD(或CD的延长线)于点F.①若BE:EC=1:9,求CF的长;
②若点F恰好与点D重合,请在备用图上画出图形,并求BE的长.