初中数学浙教版八年级上册第二章 特殊三角形 章末检测
试卷更新日期:2019-08-31 类型:单元试卷
一、单选题
-
1. 下列四个手机品牌商标中,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,∠AOB=30°,OC为∠AOB内部一条射线,点P为射线OC上一点,OP=4,点M、N分别为OA、OB边上动点,则△MNP周长的最小值为( )
2. 如图,∠AOB=30°,OC为∠AOB内部一条射线,点P为射线OC上一点,OP=4,点M、N分别为OA、OB边上动点,则△MNP周长的最小值为( )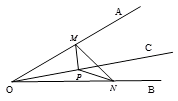 A、2 B、4 C、 D、3. 已知一个等腰三角形有两内角的度数之比为1:4,则这个等腰三角形顶角的度数为( )
A、2 B、4 C、 D、3. 已知一个等腰三角形有两内角的度数之比为1:4,则这个等腰三角形顶角的度数为( )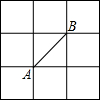 A、
A、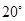 B、
B、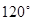 C、
C、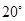 或
或 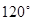 D、
D、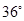 4. 如图,△ABC中,AB=AC,AD⊥BC,下列结论中不正确的是( )
4. 如图,△ABC中,AB=AC,AD⊥BC,下列结论中不正确的是( ) A、D是BC中点 B、AD平分∠BAC C、AB=2BD D、∠B=∠C5. 由下列条件可以作出等腰三角形的是( )A、已知等腰三角形的两腰 B、已知一腰和一腰上的高 C、已知底角的度数和顶角的度数 D、已知底边长和底边上的中线的长6. 已知△ABC的三边长分别为4、4、6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )条.A、3 B、4 C、5 D、67. 下列各命题的逆命题成立的是( )A、同位角相等,两直线平行 B、全等三角形的对应角相等 C、如果两个数相等,那么它们的绝对值相等 D、如果两个角都是45°,那么这两个角相等8. 如图,AC⊥BC, 若AB=5, AC=3, BC=4,下列说法错误的是( )
A、D是BC中点 B、AD平分∠BAC C、AB=2BD D、∠B=∠C5. 由下列条件可以作出等腰三角形的是( )A、已知等腰三角形的两腰 B、已知一腰和一腰上的高 C、已知底角的度数和顶角的度数 D、已知底边长和底边上的中线的长6. 已知△ABC的三边长分别为4、4、6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )条.A、3 B、4 C、5 D、67. 下列各命题的逆命题成立的是( )A、同位角相等,两直线平行 B、全等三角形的对应角相等 C、如果两个数相等,那么它们的绝对值相等 D、如果两个角都是45°,那么这两个角相等8. 如图,AC⊥BC, 若AB=5, AC=3, BC=4,下列说法错误的是( ) A、三角形ABC是直角三角形 B、C到AB的距离为4 C、B到AC的距离为4 D、A到BC的距离为39. 如图,在△ABC中,∠A=60°,BE⊥AC,垂足为E,CF⊥AB,垂足为F,点D是BC的中点,BE,CF交于点M,如果CM=4,FM=5,则BE等于( )
A、三角形ABC是直角三角形 B、C到AB的距离为4 C、B到AC的距离为4 D、A到BC的距离为39. 如图,在△ABC中,∠A=60°,BE⊥AC,垂足为E,CF⊥AB,垂足为F,点D是BC的中点,BE,CF交于点M,如果CM=4,FM=5,则BE等于( )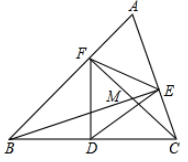 A、14 B、13 C、12 D、1110. 如图,在边长为1的正方形组成的网格图中标有 、 、 、 四条线段,其中能构成一个直角三角形三边的线段是( )
A、14 B、13 C、12 D、1110. 如图,在边长为1的正方形组成的网格图中标有 、 、 、 四条线段,其中能构成一个直角三角形三边的线段是( ) A、 , , B、 , , C、 , , D、 , ,
A、 , , B、 , , C、 , , D、 , ,二、填空题
-
11. 等腰三角形中,已知两边的长分别是9和6,则周长为 .12. 命题“两直线平行,同旁内角互补”的逆命题是 .13. 在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若BD=2,CD=1,则AC的长是。
 14. 若直角三角形的两边分别为1分米和2分米,则斜边上的中线长为.15. 定义:等腰三角形的顶角与一个底角的度数的比值称为这个等腰三角形的“特征值”,记作k,等腰△ABC中,若 ,则它的特征值k=.16. 如图,正方形ABCD的边长为2,其面积标记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2 , ……按照此规律继续下去,则S2019的值为.
14. 若直角三角形的两边分别为1分米和2分米,则斜边上的中线长为.15. 定义:等腰三角形的顶角与一个底角的度数的比值称为这个等腰三角形的“特征值”,记作k,等腰△ABC中,若 ,则它的特征值k=.16. 如图,正方形ABCD的边长为2,其面积标记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2 , ……按照此规律继续下去,则S2019的值为.
三、解答题
-
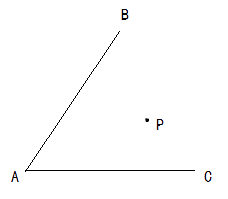
17. 有一个养鱼专业户,在如图所示地形的两个池塘里养鱼,他每天早上要从住处P分别前往两个池塘投放鱼食,试问他怎样走才能以最短距离回到住地?(请用尺规作图,保留作图痕迹,不写做法)
 18. 如图,四边形 中, , .
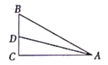
18. 如图,四边形 中, , .求证: .
 19. 如图,△ABC是等腰三角形,∠B=∠C,AD是底边BC上的高,DE∥AB交AC于点E.试说明△ADE是等腰三角形.
19. 如图,△ABC是等腰三角形,∠B=∠C,AD是底边BC上的高,DE∥AB交AC于点E.试说明△ADE是等腰三角形. 20. 如图,△ABC ≌ △ADE,∠BAD = 60°.求证:△ACE是等边三角形.
20. 如图,△ABC ≌ △ADE,∠BAD = 60°.求证:△ACE是等边三角形. 21. 如图,在△ABC中,∠ACB=90°,CD是高.
21. 如图,在△ABC中,∠ACB=90°,CD是高. (1)、图中有几个直角三角形?是哪几个?(2)、∠1和∠A有什么关系?∠2和∠A呢?还有哪些锐角相等.
(1)、图中有几个直角三角形?是哪几个?(2)、∠1和∠A有什么关系?∠2和∠A呢?还有哪些锐角相等.
22. 在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米. (1)、问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;(2)、求原来的路线AC的长.23. 如图,在 中, , ,AD是 的角平分线, ,垂足为E.
(1)、问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;(2)、求原来的路线AC的长.23. 如图,在 中, , ,AD是 的角平分线, ,垂足为E.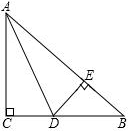 (1)、求证: ;(2)、已知 ,求AC的长;(3)、求证: .24. 如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°点D从点C出发沿CA方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.
(1)、求证: ;(2)、已知 ,求AC的长;(3)、求证: .24. 如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°点D从点C出发沿CA方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.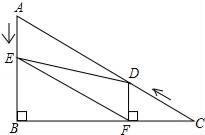 (1)、DF=;(用含t的代数式表示)(2)、求证:△AED≌△FDE;(3)、当t为何值时,△DEF是等边三角形?说明理由;(4)、当t为何值时,△DEF为直角三角形?(请直接写出t的值.)
(1)、DF=;(用含t的代数式表示)(2)、求证:△AED≌△FDE;(3)、当t为何值时,△DEF是等边三角形?说明理由;(4)、当t为何值时,△DEF为直角三角形?(请直接写出t的值.)