初中数学人教版九年级上学期 第二十二章 22.3 实际问题与二次函数
试卷更新日期：2019-08-31 类型：同步测试
一、实际应用
-
1. 某农场拟建两间矩形饲养室，一面靠足够长的墙体，中间用一道围栏隔开，并在如图8所示的三处各留1m宽的门，所有围栏的总长（不含门）为27m，则能建成的饲养室面积最大为（ ）
A、75m2 B、 m2 C、48m2 D、 m22. 一种包装盒的设计方法如图所示，四边形ABCD是边长为30cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A，B，C，D四点重合于图中的点O，形成一个底面为正方形的长方体包装盒．设BE=CF=xcm，要使包装盒的侧面积最大，则x应取（ ）
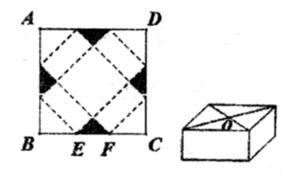A、12.5cm B、10cm C、7.5cm D、5cm3. 济南建邦大桥有一段抛物线型的拱梁，抛物线的表达式为y=ax2+bx．小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC，当小强骑自行车行驶10秒时和26秒时拱梁的高度相同，则小强骑自行车通过拱梁部分的桥面OC共需秒．
4. 在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用 长的篱笆围成一个矩形花园 （篱笆只围 、 两边）.设 ，若在 处有一棵树与墙 、 的距离分别是 和 ，要将这棵树围在花园内（含边界，不考虑树的粗细），则花园面积 的最大值为 .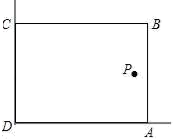
5. 某农场拟建两间矩形饲养室，一面靠现有墙(墙足够长)，中间用一道墙隔开，并在如图所示的三处各留1 m宽的门．已知计划中的材料可建墙体(不包括门)总长为27 m，则能建成的饲养室面积最大为m2 ．
6. 某灯具厂生产并销售A，B两种型号的智能台灯共100盏，生产并销售一盏A型智能台灯可以获利30元；如果生产并销售不超过20盏B型台灯，则每盏B型台灯可以获利90元，如果超出20盏B型台灯，则每超出1盏，每盏B型台灯获利将均减少2元．设生产并销售B型台灯x盏．（其中x>20）(1)、完成下列表格：
(2)、当A型台灯所获得的利润比B型台灯所获得利润少200元时，求生产并销售A，B两种台灯各多少盏？(3)、如何设计生产销售方案可以获得最大利润，最大的利润为多少元？7. 某公司为一工厂代销一种建筑材料（这里的代销是指厂家先免费提供货源，待货物售出后再进行结算，未售出的由厂家负责处理）．当每吨售价为260元时，月销售量为45吨．该经销店为提高经营利润，准备采取降价的方式进行促销．经市场调查发现：当每吨售价每下降10元时，月销售量就会增加7.5吨．综合考虑各种因素，每售出一吨建筑材料共需支付厂家及其它费用100元．设每吨材料售价为x（元），该经销店的月利润为y（元）．当每吨售价是240元时，计算此时的月销售量；(1)、求出 y 与x的函数关系式（不要求写出x 的取值范围）；(2)、该经销店要获得最大月利润，售价应定为每吨多少元？(3)、小静说：“当月利润最大时，月销售额也最大．”你认为对吗？请说明理由．8. 某商品的进价为每件50元，当售价为每件70元时，每星期可卖出150件，现需降价处理，且经市场调查：每降价2元，每星期可多卖出20件，在确保盈利的前提下，解答下列问题：(1)、若设每件降价x元、每星期售出商品的利润为y元，请写出y与x的函数关系式，并求出自变量x的取值范围；(2)、当降价多少元时，每星期的利润最大？最大利润是多少？二、真题演练
-
9. 如图，利用一个直角墙角修建一个梯形储料场ABCD，其中∠C＝120°.若新建墙BC与CD总长为12m，则该梯形储料场ABCD的最大面积是（ ）
A、18m2 B、 m2 C、 m2 D、 m210. 有一块形状如图的五边形余料ABCDE，AB=AE=6，BC=5，∠A=∠B=90°， ∠C=135°. ∠E＞90°.要在这块余料中截取一块矩形材料，其中一条边在AE上，并使所截矩形材料的面积尽可能大。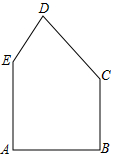
(1)、若所截矩形材料的一条边是BC或AE，求矩形材料的面积。(2)、能否数出比（1）中更大面积的矩形材料？如果能，求出这些矩形材料面积的最大值；如果不能，说明理由.11. “互联网+”时代，网上购物备受消费者青睐.某网店专售一款休闲裤，其成本为每条40元，当售价为每条80元时，每月可销售100条.为了吸引更多顾客，该网店采取降价措施.据市场调查反映：销售单价每降1元，则每月可多销售5条.设每条裤子的售价为x元（x为正整数），每月的销售量为y条.(1)、直接写出y与x的函数关系式；(2)、设该网店每月获得的利润为w元，当销售单价降低多少元时，每月获得的利润最大，最大利润是多少？(3)、该网店店主热心公益事业，决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元，且让消费者得到最大的实惠，该如何确定休闲裤的销售单价？