初中数学人教版九年级上学期第二十二章 22.2 二次函数与一元二次方程

试卷更新日期：2019-08-31 类型：同步测试

进入出卷网下载

1. 用“描点法”画二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图像时.列了如下表格：

根据表格上的信息回答问题：一元二次方程 $a x^{2} + b x + c - 5 = 0$ 的解为（）

A、 $x_{1} = - 2 ， x_{2} = 4$ B、 $x_{1} = - 1 ， x_{2} = 3$ C、 $x_{1} = 3 ， x_{2} = 4$ D、 $x_{1} = - 4 ， x_{2} = 4$

查看试题解析
2. 二次函数y＝ax²+bx+c（a≠0，a、b、c为常数）的图象如图所示，则方程ax²+bx+c＝m有实数根的条件是（）

A、m≥﹣4 B、m≥0 C、m≥5 D、m≥6

查看试题解析
3. 已知函数y=﹣（x﹣m）（x﹣n）+3，并且a，b是方程（x﹣m）（x﹣n）=3的两个根，则实数m，n，a，b的大小关系可能是（）

A、m＜a＜b＜n B、m＜a＜n＜b C、a＜m＜b＜n D、a＜m＜n＜b

查看试题解析
4. 二次函数y=ax²+bx+c（a≠0）的函数值y与自变量x的四组对应值如表所示

x

6.15

6.18

6.21

6.24

y

0.02

-0.01

0.02

0.11

则方程ax²+bx+c=0的根的个数是（）

A、0 B、1 C、2 D、不能确定

查看试题解析
5. 二次函数y＝x²+bx+c的图象如图所示，则x²+bx+c＝0的两根分别是．

查看试题解析

6. 如图，抛物线y=-x²+mx的对称轴为直线x=2，若关于x的一元二次方程-x²+mx-t=0 (t为实数)在1<x<3的范围内有解，则t的取值范围是（）

A、-5<t≤4 B、3<t≤4 C、-5<t<3 D、t>-5

查看试题解析
7. 关于x的方程x²﹣2mx+4＝0有两个不同的实根，并且有一个根小于1，另一个根大于3，则实数m的取值范围为（）

A、m＞ $\frac{5}{2}$ B、m＜﹣ $\frac{5}{2}$ C、m＜﹣2 或 m＞2 D、m＞ $\frac{13}{6}$

查看试题解析
8. 如图所示，抛物线y=ax²+bx+c的顶点为B（﹣1，3），与x轴的交点A在点（﹣3，0）和（﹣2，0）之间，以下结论：①b²﹣4ac=0，②2a﹣b=0，③a+b+c＜0；④c﹣a=3，其中正确的有（）个．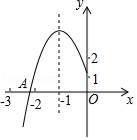

A、1 B、2 C、3 D、4

查看试题解析
9. 已知二次函数y=﹣x²+x+6及一次函数y=﹣x+m，将该二次函数在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新函数（如图所示），当直线y=﹣x+m与新图象有4个交点时，m的取值范围是（）

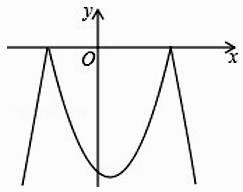A、 $- \frac{25}{4}$ ＜m＜3 B、 $- \frac{25}{4}$ ＜m＜2 C、﹣2<m<3 D、﹣6<m<﹣2

查看试题解析
10. 在平面直角坐标系中，抛物线y＝（x﹣h）²+k的对称轴是直线x＝1.

(1)、若抛物线与x轴交于原点，求k的值；

(2)、当﹣1＜x＜0时，抛物线与x轴有且只有一个公共点，求k的取值范围.

查看试题解析

11. 已知m＞0，关于x的一元二次方程（x+1）（x﹣2）﹣m＝0的解为x₁ ， x₂（x₁＜x₂），则下列结论正确的是（）

A、x₁＜﹣1＜2＜x₂ B、﹣1＜x₁＜2＜x₂ C、﹣1＜x₁＜x₂＜2 D、x₁＜﹣1＜x₂＜2

查看试题解析
12. 抛物线y＝ax²＋bx＋c经过点A(－3，0)、B(4，0)两点，则关于x的一元二次方程a(x－1)²＋c＝b－bx的解是

查看试题解析

x	6.15	6.18	6.21	6.24
y	0.02	-0.01	0.02	0.11

初中数学人教版九年级上学期 第二十二章 22.2 二次函数与一元二次方程