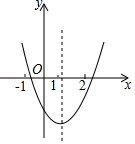初中数学人教版九年级上学期 第二十二章 22.1.4 二次函数y=ax2+bx+c的图象和性质
试卷更新日期:2019-08-31 类型:同步测试
一、基础巩固
-
1. 在下列二次函数中,其图象对称轴为x=2的是( )A、y=2x2﹣4 B、y=2(x-2)2 C、y=2x2+2 D、y=2(x+2)22. 已知点A(-1,m),B(1,m),C(2,m+1)在同一个函数图象上,这个函数图象可能是( )A、
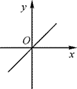 B、
B、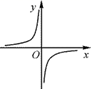 C、
C、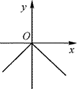 D、
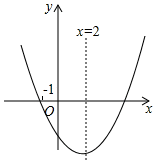
D、 3. 将 化成 的形式,则 的值是( )A、-5 B、-8 C、-11 D、54. 在二次函数 的图像中,若y随着x的增大而增大,则x的取值范围是( )A、x<1 B、x>1 C、x<2 D、x>-15. 如图所示的是二次函数 ( 为常数,且 )的图象,其对称轴为直线 ,且经过点(0,1),则下列结论错误的是( )
3. 将 化成 的形式,则 的值是( )A、-5 B、-8 C、-11 D、54. 在二次函数 的图像中,若y随着x的增大而增大,则x的取值范围是( )A、x<1 B、x>1 C、x<2 D、x>-15. 如图所示的是二次函数 ( 为常数,且 )的图象,其对称轴为直线 ,且经过点(0,1),则下列结论错误的是( ) A、 B、 C、 D、6. 给出下列函数:①y=2x-3;②y= ;③y=2x2;④y=-3x+1.上述函数中符合条件“当x>0时,函数值y随自变量x增大而增小”的是( )A、①③ B、③④ C、②④ D、②③7. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=-1,点B的坐标为(1,0),则下列结论:①AB=4;②b2-4ac>0;③ab<0;④a2-ab+ac<0,⑤b+2a=0,其中正确的结论个数是( )
A、 B、 C、 D、6. 给出下列函数:①y=2x-3;②y= ;③y=2x2;④y=-3x+1.上述函数中符合条件“当x>0时,函数值y随自变量x增大而增小”的是( )A、①③ B、③④ C、②④ D、②③7. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=-1,点B的坐标为(1,0),则下列结论:①AB=4;②b2-4ac>0;③ab<0;④a2-ab+ac<0,⑤b+2a=0,其中正确的结论个数是( )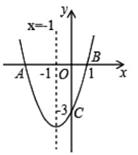 A、1个 B、2个 C、3个 D、4个8. 已知二次函数 .(1)、将解析式化成顶点式;(2)、写出它的开口方向、对称轴和顶点坐标;(3)、x取什么值时, 随 的增大而增大; 取什么值时, 随 增大而减小.
A、1个 B、2个 C、3个 D、4个8. 已知二次函数 .(1)、将解析式化成顶点式;(2)、写出它的开口方向、对称轴和顶点坐标;(3)、x取什么值时, 随 的增大而增大; 取什么值时, 随 增大而减小.二、强化提升
-
9. 二次函数y=ax2+bx+c(a、b、c为常数且a≠0)中的x与y的部分对应值如下表,该抛物线的对称轴是直线( )
x
﹣1
0
1
3
y
﹣1
3
5
3
A、x=0 B、x=1 C、x=1.5 D、x=210. 已知二次函数 y = x2- 4x + n (n 是常数),若对于抛物线上任意两点 A (x1 , y1 ) ,B (x2 , y2 ) 均有 y1>y2 ,则 x1 , x2 应满足的关系式是( )A、x1 - 2>x2 - 2 B、x1 - 2<x2 - 2 C、| x1 - 2|>|x2 - 2| D、| x1 - 2 | <|x2 - 2 |11. 如图,二次函数y=ax2+bx的图象开口向下,且经过第三象限的点P.若点P的横坐标为﹣1,则一次函数y=(a﹣b)x+b的图象大致是( )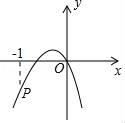 A、
A、 B、
B、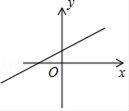 C、
C、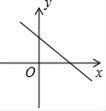 D、
D、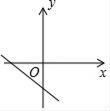 12. 对于二次函数y=x2﹣4x+4,当自变量x满足a≤x≤3时,函数值y的取值范围为0≤y≤1,则a的取值范围为.13. 已知y关于x的函数:y=(k﹣2)x2﹣2(k﹣1)x+k+1中满足k≤3.(1)、求证:此函数图象与x轴总有交点;(2)、当关于z的方程 有增根时,求上述函数图象与x轴的交点坐标.14. 如图,在平面直角坐标系中,抛物线y=ax2﹣4ax+3(a≠0)与抛物线y= +k均经过点A(1,0).直线x=m在这两条抛物线的对称轴之间(不与对称轴重合).函数y=ax2﹣4ax+3(x≥m)的图象记为G1 , 函数y= +k(x≤m)的图象记为G2 , 图象G1与G2合起来得到的图形记为G.
12. 对于二次函数y=x2﹣4x+4,当自变量x满足a≤x≤3时,函数值y的取值范围为0≤y≤1,则a的取值范围为.13. 已知y关于x的函数:y=(k﹣2)x2﹣2(k﹣1)x+k+1中满足k≤3.(1)、求证:此函数图象与x轴总有交点;(2)、当关于z的方程 有增根时,求上述函数图象与x轴的交点坐标.14. 如图,在平面直角坐标系中,抛物线y=ax2﹣4ax+3(a≠0)与抛物线y= +k均经过点A(1,0).直线x=m在这两条抛物线的对称轴之间(不与对称轴重合).函数y=ax2﹣4ax+3(x≥m)的图象记为G1 , 函数y= +k(x≤m)的图象记为G2 , 图象G1与G2合起来得到的图形记为G. (1)、求a、k的值.(2)、当m= 时,求图形G上y随x的增大而减小时x的取值范围.(3)、当﹣2≤x≤ 时,图形G上最高点的纵坐标为2,求m的值.(4)、当直线y=2m﹣1与图形G有2个公共点时,直接写出m的取值范围.15. 如图,已知点A(0,2),B(2,2),C(﹣1,﹣2),抛物线F:y=x2﹣2mx+m2﹣2与直线x=﹣2交于点P.
(1)、求a、k的值.(2)、当m= 时,求图形G上y随x的增大而减小时x的取值范围.(3)、当﹣2≤x≤ 时,图形G上最高点的纵坐标为2,求m的值.(4)、当直线y=2m﹣1与图形G有2个公共点时,直接写出m的取值范围.15. 如图,已知点A(0,2),B(2,2),C(﹣1,﹣2),抛物线F:y=x2﹣2mx+m2﹣2与直线x=﹣2交于点P. (1)、当抛物线F经过点C时,求它的表达式;(2)、设点P的纵坐标为yP , 求yP的最小值,此时抛物线F上有两点(x1 , y1),(x2 , y2),且x1<x2≤﹣2,比较y1与y2的大小;
(1)、当抛物线F经过点C时,求它的表达式;(2)、设点P的纵坐标为yP , 求yP的最小值,此时抛物线F上有两点(x1 , y1),(x2 , y2),且x1<x2≤﹣2,比较y1与y2的大小;
(3)、当抛物线F与线段AB有公共点时,直接写出m的取值范围.
三、真题演练
-
16. 如图,抛物线y=ax2+bx+c的对称轴为直线x=1,则下列结论中,错误的是( )
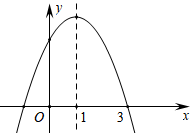 A、 B、 C、 D、
A、 B、 C、 D、