初中数学浙教版八年级上册2.6 直角三角形 同步训练
试卷更新日期:2019-08-31 类型:同步测试
一、直角三角形两个锐角互余
-
1. 将两块直角三角尺的直角顶点重合为如图的位置,若∠AOC=20°,则∠BOD=( )
 A、10° B、20° C、70° D、80°2. 如图,在▱ABCD中,AE⊥CD于点E,∠B=65°,则∠DAE等于( )
A、10° B、20° C、70° D、80°2. 如图,在▱ABCD中,AE⊥CD于点E,∠B=65°,则∠DAE等于( ) A、15° B、25° C、35° D、65°3. 如图,直角△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F.
A、15° B、25° C、35° D、65°3. 如图,直角△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F. (1)、求证:CD∥EF;(2)、若∠FEC=25°,求∠A的度数.
(1)、求证:CD∥EF;(2)、若∠FEC=25°,求∠A的度数.二、直角三角形斜边上的中线
-
4. 如图,O为线段AB的中点,AB=4cm,P1、P2、P3、P4到点O的距离分别是1cm、2cm、2.8cm、1.7cm,下列四点中能与A、B构成直角三角形的顶点是( )
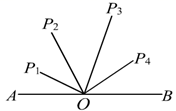 A、P1 B、P2 C、P3 D、P45. 如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连接AE.若BD=13,则AC=.
A、P1 B、P2 C、P3 D、P45. 如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连接AE.若BD=13,则AC=. 6. 如图,在△ABC中,BC=9,AD是BC边上的高,M、N分别是AB、AC边的中点,DM=5,DN=3,则△ABC的周长是 .
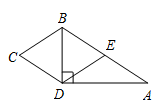
6. 如图,在△ABC中,BC=9,AD是BC边上的高,M、N分别是AB、AC边的中点,DM=5,DN=3,则△ABC的周长是 . 7. 已知:如图,四边形ABCD中,∠ABC=90°,∠ADC=90°,点E为AC中点,点F为BD中点.求证:EF⊥BD
7. 已知:如图,四边形ABCD中,∠ABC=90°,∠ADC=90°,点E为AC中点,点F为BD中点.求证:EF⊥BD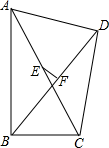 8. 小明在学完北师大数学八年级(下)第一章后,看到这样一道题目:“已知,如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,求证:MN⊥BD”.小明思考片刻,找到了解决方法,他做了辅助线。聪明的你知道他做的辅助线是什么吗?怎么证明的?小明又突然想到,在边AD上能找一点P,使得PB=PD,请你写出证明过程。
8. 小明在学完北师大数学八年级(下)第一章后,看到这样一道题目:“已知,如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,求证:MN⊥BD”.小明思考片刻,找到了解决方法,他做了辅助线。聪明的你知道他做的辅助线是什么吗?怎么证明的?小明又突然想到,在边AD上能找一点P,使得PB=PD,请你写出证明过程。 9. 如图,在Rt△ACB中,∠ACB=90º,点D是AB的中点,点E是CD的中点,过C作CF∥AB交AE的延长线于点F,连BF.
9. 如图,在Rt△ACB中,∠ACB=90º,点D是AB的中点,点E是CD的中点,过C作CF∥AB交AE的延长线于点F,连BF. (1)、求证:△ADE≌△FCE;(2)、若∠DCF=120º,DE=2,求BC的长.
(1)、求证:△ADE≌△FCE;(2)、若∠DCF=120º,DE=2,求BC的长.三、含30度角的直角三角形
-
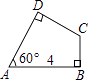
10. 若等腰三角形的底角为15°,则一腰上的高是腰长的( )A、 B、 C、1倍 D、2倍11. 如图由于台风的影响,一棵树在离地面 处折断,折断后树干上部分与地面成30度的夹角,折断前长度是 ( )
 A、 B、 C、 D、 .12. 在Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2,则AB的长是( )A、2 B、4 C、8 D、1613. 如图所示, 中, , , 的垂直平分线 交 于点 ,交 于点 .求证: .
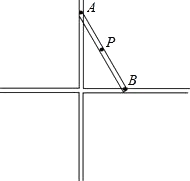
A、 B、 C、 D、 .12. 在Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2,则AB的长是( )A、2 B、4 C、8 D、1613. 如图所示, 中, , , 的垂直平分线 交 于点 ,交 于点 .求证: . 14. 已知:在一个直角三角形中30°角所对的直角边为3cm,则斜边长为 .15. 如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PD=3cm,则PC的长为cm.
14. 已知:在一个直角三角形中30°角所对的直角边为3cm,则斜边长为 .15. 如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PD=3cm,则PC的长为cm.
四、直角三角形的判定
-
16. 已知△ABC中,∠A=20°,∠B=70°,那么△ABC是( )A、直角三角形 B、锐角三角形 C、钝角三角形 D、正三角形17. 在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,△ABD和△AFD关于直线AD对称,∠FAC的平分线交BC于点G,连接FG.
 (1)、求∠DFG的度数;(2)、设∠BAD=θ,
(1)、求∠DFG的度数;(2)、设∠BAD=θ,①当θ为何值时,△DFG为等腰三角形;
②△DFG有可能是直角三角形吗?若有,请求出相应的θ值;若没有,请说明理由.
五、中考演练
-
18. 如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=1,则BC的长为( )
 A、4 B、6 C、 D、8
A、4 B、6 C、 D、8