初中数学人教版八年级上学期 第十二章 12.3 角的平分线的性质
试卷更新日期：2019-08-31 类型：同步测试
一、基础巩固
-
1. 过线段AB外一点C，用直尺和圆规作AB的垂线段CD，以下四个作图中，作法错误的是（ ）A、
B、
C、
D、
2. 如图，已知AB∥CD，EF平分∠CEG，∠1=80°，则∠2的度数为 （ ）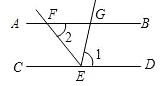
A、20° B、40° C、50° D、60°3. 如图，已知△ABC中，∠C=90°，AD平分∠BAC，且CD：BD=3：4.若BC=21，则点D到AB边的距离为（ ）
A、7 B、9 C、11 D、144. 如图，在△ABC中，∠C＝90°，∠B＝30°，AD是∠BAC的角平分线，DE⊥AB，垂足为E，DE＝1，则BC＝ ．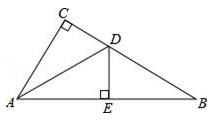
5. 如图，在Rt△ABC中，∠C＝90°，以A为圆心，任意长为半径画弧，分别交AC ， AB于点M ， N；再分别以M ， N为圆心，以大于 MN的长为半径画弧，两弧交于点G；作射线AG交BC于点D ， 若CD＝2，BD＝2.5，P为AB上一动点，则PD的最小值为 ．
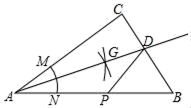6. 如图，在△ABC中，∠ACB＝90°，AD是△ABC的角平分线，BC＝10cm，BD：DC＝3：2，则点D到AB的距离为 ．
7. 尺规作图：作点A关于直线l的对称点A'.已知：直线l和l外一点A.
求作：点A关于l的对称点A'.
作法：①在l上任取一点P，以点P为圆心，PA长为半径作孤，交l于点B；②以点B为圆心，AB长为半径作弧，交弧AB于点A'. 点A'就是所求作的对称点.
由步骤①，得
由步骤②，得
将横线上的内容填写完整，并说明点A与A'关于直线l对称的理由.
8. 如图.在△ABC中，AD是角平分线，且BD=CD，DE⊥AB，DF⊥AC，垂足分别为E、F.求证：EB=FC.
9. 如图AB=AC，BD=CD，DE⊥BA，点E为垂足，DF⊥AC，点F为垂足，求证：DE=DF．
二、强化提升
-
10. 如图，在ΔABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于D，DE⊥AB于E，若AB=6cm，则ΔDBE的周长是（ ）
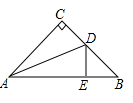A、6cm B、7cm C、8cm D、9 cm11. 如图，在四边形ABCD中，对角线AC平分∠DAB，∠ABD=52°，∠ABC=116°，∠ACB=α°，则∠BDC的度数为（ ）
A、α B、
C、90﹣α
D、90﹣ α
12. 如图，在△ABC中，∠C=90°，AD平分∠BAC交BC于点D，DE⊥AB于点E，则下列结论：①AD平分∠CDE；②∠BAC=∠BDE；③DE平分∠ADB；④若AC=4BE，则S△ABC=8S△BDE其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个13. 如图，在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB于E，有下列结论：①CD=ED；②AC+BE=AB；③∠BDE=∠BAC；④AD平分∠CDE；⑤S△ABD：S△ACD=AB：AC，其中正确的有（ ）
A、5个 B、4个 C、3个 D、2个14. 如图，BD平分∠ABC，DE⊥AB于E，DF⊥BC于F，AB=6，BC=8.若S△ABC=28，则DE=
15. 如图，在∠AOB 的边 OA、OB 上取点 M、N，连接 MN，P 是△MON 外角平分线的交点， 若 MN=2， ， ． 则△MON 的周长是；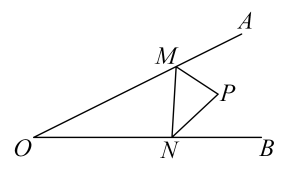
16. 如图，DE∥BC，DF、BE分别平分∠ADE、∠ABC，求证：∠FDE=∠DEB。
17. 如图，在△ABC中，∠ACB＝90°，CE⊥AB于点E，AD＝AC，AF平分∠CAB交CE于点F，DF的延长线交AC于点G，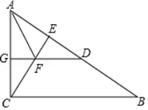
求证：
(1)、DF∥BC；(2)、FG＝FE．三、真题演练
-
18. 如图.在△ABC中，AC=BC，∠A=40°，观察图中尺规作图的痕迹，可知∠BCG的度数为（ ）
A、40° B、45° C、50° D、60°19. 如图，在 和 中， ，连接 交于点 ，连接 ．下列结论：① ；② ；③ 平分 ；④ 平分 ．其中正确的个数为（ ）．
A、4 B、3 C、2 D、120. 已知：∠AOB.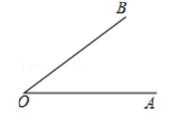
求作：∠A'O'B'，使得A'O'B'=∠AOB.
作法：
①以O为圆心，任意长为半径画弧，分别交OA，OB于点C，D；
②画一条射线O'A'，以点O'为圆心，OC长为半径画弧，交O'A'于点C'；
③以点C'为圆心，CD长为半径画弧，与第②步中所画的弧相交于点D'；
④过点D'画射线O'B'，则∠A'O'B'=∠AOB.
根据上面的作法，完成以下问题：
(1)、使用直尺和圆规，作出∠A'O'B' (请保留作图痕迹).(2)、完成下面证明∠A'O'B'=∠AOB的过程(注：括号里填写推理的依据).证明：由作法可知O'C'=OC，O'D'=OD，D'C'= ，
∴△C'O'D'≌△COD
∴∠A'O'B'= ∠AOB.