初中数学浙教版八年级上册第一章 三角形的初步认识 章末检测
试卷更新日期:2019-08-31 类型:单元试卷
一、单选题
-
1. 下列图形是全等图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,∠B=∠C,∠1=∠3,则∠1与∠2之间的关系是( )
2. 如图,∠B=∠C,∠1=∠3,则∠1与∠2之间的关系是( )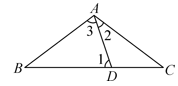 A、∠1=2∠2 B、3∠1﹣∠2=180° C、∠1+3∠2=180° D、2∠1+∠2=180°3. 下列说法正确的是( )A、全等三角形是指形状相同的两个三角形 B、全等三角形是指面积相等的两个三角形 C、两个等边三角形是全等三角形 D、全等三角形是指两个能完全重合的三角形4. 如图, BD 是△ABC 的角平分线, AE⊥ BD ,垂足为 F .若∠ABC=35°,∠ C=50°,则∠CDE 的度数为( )
A、∠1=2∠2 B、3∠1﹣∠2=180° C、∠1+3∠2=180° D、2∠1+∠2=180°3. 下列说法正确的是( )A、全等三角形是指形状相同的两个三角形 B、全等三角形是指面积相等的两个三角形 C、两个等边三角形是全等三角形 D、全等三角形是指两个能完全重合的三角形4. 如图, BD 是△ABC 的角平分线, AE⊥ BD ,垂足为 F .若∠ABC=35°,∠ C=50°,则∠CDE 的度数为( ) A、35° B、40° C、45° D、50°5. 已知 是 的三边长,化简 的值是( )A、 B、 C、 D、6. 已知下图中的两个三角形全等,则∠α度数是( )
A、35° B、40° C、45° D、50°5. 已知 是 的三边长,化简 的值是( )A、 B、 C、 D、6. 已知下图中的两个三角形全等,则∠α度数是( )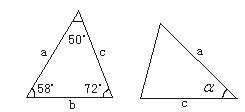 A、72° B、60° C、58° D、50°7. 下列有关三角形全等的判定,错误的是( )A、三边分别相等的两个三角形全等(SSS) B、两边和它们的夹角分别相等的两个三角形全等(SAS) C、两角和它们的夹边分别相等的两个三角形全等(ASA) D、两边及其中一边的对角对应相等的两个三角形全等(SSA)8. 如图,在△ABC中,∠B=50°,∠C=30°,分别以点A和点C为圆心,大于 AC的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,则∠BAD的度数为( )
A、72° B、60° C、58° D、50°7. 下列有关三角形全等的判定,错误的是( )A、三边分别相等的两个三角形全等(SSS) B、两边和它们的夹角分别相等的两个三角形全等(SAS) C、两角和它们的夹边分别相等的两个三角形全等(ASA) D、两边及其中一边的对角对应相等的两个三角形全等(SSA)8. 如图,在△ABC中,∠B=50°,∠C=30°,分别以点A和点C为圆心,大于 AC的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,则∠BAD的度数为( )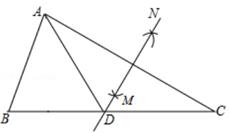 A、50° B、60° C、70° D、80°9. 用直尺和圆规作一个角等于已知角的示意图如图,则说明∠D′O′C′=∠DOC的依据是( )
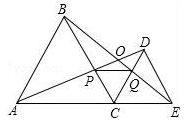
A、50° B、60° C、70° D、80°9. 用直尺和圆规作一个角等于已知角的示意图如图,则说明∠D′O′C′=∠DOC的依据是( )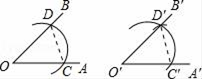 A、SSS B、SAS C、ASA D、AAS10. 如图所示,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下四个结论:①△ACD≌△BCE;②AD=BE;③∠AOB=60°;④△CPQ是等边三角形.
A、SSS B、SAS C、ASA D、AAS10. 如图所示,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下四个结论:①△ACD≌△BCE;②AD=BE;③∠AOB=60°;④△CPQ是等边三角形.其中正确的是( )
 A、①②③④ B、②③④ C、①③④ D、①②③
A、①②③④ B、②③④ C、①③④ D、①②③二、填空题
-
11. 对于命题“如果∠1+∠2=90°,那么∠1=∠2”,能说明它是假命题的反例是 .12. 两条平行线被第三条直线所截,一对内错角的角平分线的位置关系是.13. 下列命题中:
①若 ,则 ;②两直线平行,同位角相等;③对顶角相等;④内错角相等,两直线平行.是真命题的是.(填写所有真命题的序号)
14. 已知:直线l1∥l2 , 一块含30°角的直角三角板如图所示放置,∠1=25°,则∠2等于 .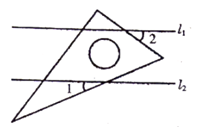 15. 如图,△ABC沿直线AB向下平移可以得到△DEF,如果AB=8,BD=5,那么BE等于。
15. 如图,△ABC沿直线AB向下平移可以得到△DEF,如果AB=8,BD=5,那么BE等于。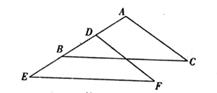 16. 下面三个命题: 底边和顶角对应相等的两个等腰三角形全等; 两边及其中一边上的中线对应相等的两个三角形全等; 斜边和斜边上的中线对应相等的两个直角三角形全等,其中正确的命题的序号为 .
16. 下面三个命题: 底边和顶角对应相等的两个等腰三角形全等; 两边及其中一边上的中线对应相等的两个三角形全等; 斜边和斜边上的中线对应相等的两个直角三角形全等,其中正确的命题的序号为 .三、综合题
-
17. 如图,直线CD与直线AB相交于C,根据下列语句画图、解答。(1)、过点P作PQ∥CD,交AB于点Q(2)、过点P作PR⊥CD,垂足为R(3)、若∠DCB=120°,猜想∠PQC是多少度?并说明理由
18. 尺规作图:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵桂花树.如图,要求桂花树的位置(视为点P),到花坛的两边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种桂花树的位置点P(不写作法,保留作图痕迹).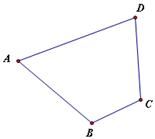 19. 如图,是一块破损的木板.
19. 如图,是一块破损的木板.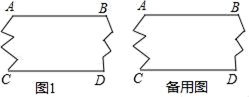
(1)、请你设计一种方案,检验木板的两条直线边缘AB、CD是否平行;
(2)、若AB∥CD,连接BC,过点A作AM⊥BC于M,垂足为M,画出图形,并写出∠BCD与∠BAM的数量关系.20. 如图,是一个4×4的方格,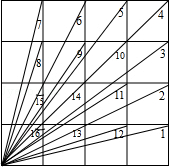 (1)、求图中∠1+∠2+∠3+∠4+…+∠16的和.(2)、求∠1﹣∠2+∠3﹣∠4+…+∠15﹣∠16.21. 如图, , , ,求 .
(1)、求图中∠1+∠2+∠3+∠4+…+∠16的和.(2)、求∠1﹣∠2+∠3﹣∠4+…+∠15﹣∠16.21. 如图, , , ,求 .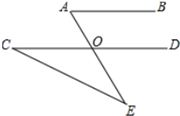 22. 阅读理解题:如图,有一池塘,要测量两端A、B的距离,设计了如下方案:先在平地上取一个点可直接到达A、B的点O,延长AO到C,使CO=AO,延长BO到D,使DO=BO,连结DC并量出它的长度,DC的长度就是A、B两点的距离。此方案是否合理?请说明理由。
22. 阅读理解题:如图,有一池塘,要测量两端A、B的距离,设计了如下方案:先在平地上取一个点可直接到达A、B的点O,延长AO到C,使CO=AO,延长BO到D,使DO=BO,连结DC并量出它的长度,DC的长度就是A、B两点的距离。此方案是否合理?请说明理由。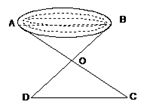 23. 如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F。
23. 如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F。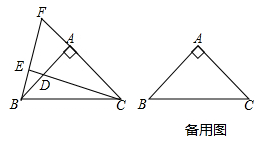 (1)、点D在边AB上时,试探究线段BD、AB和AF的数量关系,并证明你的结论;(2)、点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请写出正确结论并证明。24. 数学思维是数学地思考问题和解决问题,运用数学概念,思维和方法,辨明数学关系,形成良好的思维品质,试用你的数学能力解决下列问题:
(1)、点D在边AB上时,试探究线段BD、AB和AF的数量关系,并证明你的结论;(2)、点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请写出正确结论并证明。24. 数学思维是数学地思考问题和解决问题,运用数学概念,思维和方法,辨明数学关系,形成良好的思维品质,试用你的数学能力解决下列问题: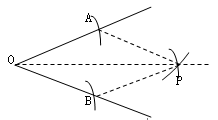 图 1
图 1  图 2(1)、如图 1 是角平分线的一种作法,其运用的数学知识是全等三角形判定方法中的(判定方法);
图 2(1)、如图 1 是角平分线的一种作法,其运用的数学知识是全等三角形判定方法中的(判定方法);
(2)、如图 2,在△ABC 中,∠B=60°,∠BAC 的平分线 AD 与∠BCA 的平分线 CE 交于点 F, 则:①∠AFC=度.
②写出EF与FD的数量关系,并说明理由;