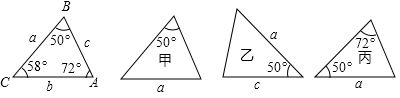
初中数学浙教版八年级上册1.5 三角形全等的判定：AAS和角平分线 同步训练
试卷更新日期：2019-08-31 类型：同步测试
一、角平分线
-
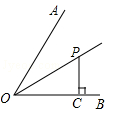
1. 如图，OP为∠AOB的平分线，PC⊥OB于点C，且PC=3，点P到OA的距离为 ．
2. 完成下面的证明：如图，∠C=50°，E是BA延长线上的一点，过点A作 //BC﹒若AD平分∠CAE，求∠B的度数．
解：∵ //BC，∠C=50°（ 已知 ），
∴∠2==°（）.
又∵AD平分∠CAE（ 已知 ），
∴=∠2=50°（）.
又∵ //BC（已知），
∴∠B==°（）.
3. 如图，在△ABC中，DE是AC的垂直平分线，AC=6cm，且△ABD的周长为13cm，则△ABC的周长为（ ）cm．
A、19 B、13 C、10 D、164. 如图，在△BC中，已知AD是∠BAC的平分线，且AB=AC+CD，若∠BAC=60°，则∠ABC的大小为（ ）
A、30° B、40° C、45° D、50°5. 如图所示，已知△ABC的周长是20，OB、OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD=3，则△ABC的面积是 ．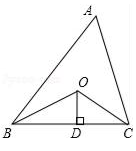
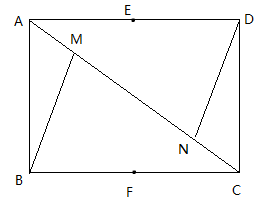
6. 电信部门要修建一座电视信号发射塔P，按照设计要求，发射塔P到两城镇A、B的距离必须相等，到两条高速公路m和n的距离也必须相等．请在图中作出发射塔P的位置．（尺规作图，不写作法，保留作图痕迹）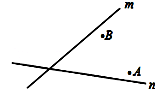
7. 如图，在△ABC中，DM、EN分别垂直平分AC和BC，交AB于M、N两点，DM与EN相交于点F．
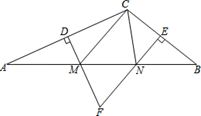(1)、若△CMN的周长为15cm，求AB的长；(2)、若∠MFN=70°，求∠MCN的度数．二、AAS
-
8. 如图，已知 ，添加条件后，可得 ，则在下列条件中，不能添加的是（ ）
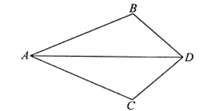A、 B、 C、 D、9. 如图，AB⊥BC，OB=OC，CD⊥BC，点A，O，D在一条直线上，通过测量CD的长可知小河的宽AB.由此判定△AOB≌△DOC的依据是（ ）
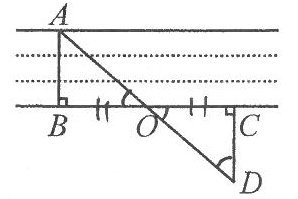A、SAS或SSA B、ASA或AAS C、SAS或ASA D、SSS或AAS10. 如图，∠1=∠2，AB=AD，点E在边BC上，∠C=∠AED，AB与DE交于点O.
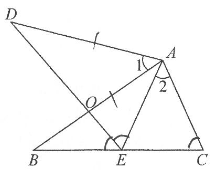(1)、求证：△ABC≌△ADE；(2)、当∠1=40°时，求∠BED的度数.11. 如图，已知 ， ，增加下列条件：① ；② ；③ ；④ .其中能使 的条件有（ ）
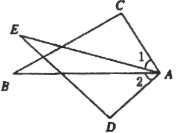A、4个 B、3个 C、2个 D、1个12. 如图， 、 、 三点在同一条直线上， ， ， .
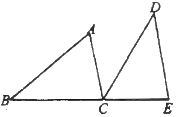(1)、求证： ；(2)、若 ，求 的度数.13. 已知：如图，AC、BD相交于点E，AB=DC，∠B=∠C.
求证：
(1)、△ABE≌△DCE；(2)、∠BDA=∠CAD.14. 如图，△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于F，若BF=AC，那么∠ABC的大小是（ ）
A、40° B、45° C、50° D、60°三、中考演练
-
15. 如图，已知 ，求证： .
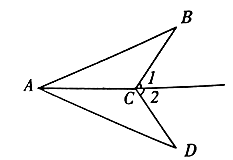16. 如图，AB∥CD，E、F分别为AB、CD上的点，且EC∥BF，连接AD，分别与EC、BF相交与点G、H，若AB＝CD，求证：AG＝DH．
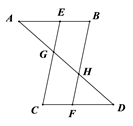17. 如图，在 和 中， ，连接 交于点 ，连接 ．下列结论：① ；② ；③ 平分 ；④ 平分 ．其中正确的个数为（ ）．
A、4 B、3 C、2 D、1
