初中数学浙教版八年级上册 1.5 三角形全等的判定:ASA 同步训练
试卷更新日期:2019-08-31 类型:同步测试
一、基础夯实
-
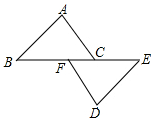
1. 如图,点B,F,C,E在一条直线上,FB=CE,AB∥ED,AC∥FD。求证:AB=DE, AC=DF.
 2. 如图, , ,AC与BD相交于点 求证: .
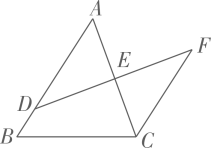
2. 如图, , ,AC与BD相交于点 求证: .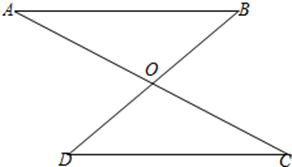 3. 如图,点B、E、C、F在同一直线上,∠A=∠D,AB∥DE,BE=CF.求证:AC=DF.
3. 如图,点B、E、C、F在同一直线上,∠A=∠D,AB∥DE,BE=CF.求证:AC=DF. 4. 已知:如图,点E,A,C在同一直线上,AB∥CD,AB=CE,AC=CD.
4. 已知:如图,点E,A,C在同一直线上,AB∥CD,AB=CE,AC=CD.求证:BC=ED.
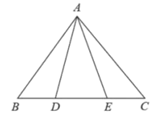
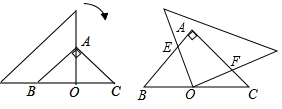
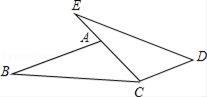 5. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块)你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带.依据
5. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块)你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带.依据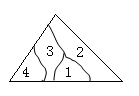
二、提高特训
-
6. 如图,AB=DB,∠1=∠2,请问添加下面哪个条件不能判断△ABC≌△DBE的是( )
 A、BC=BE B、∠A=∠D C、∠ACB=∠DEB D、AC=DE7. 如图,G是△ABC的重心,直线L过A点与BC平行.若直线CG分别与AB,L交于D,E两点,直线BG与AC交于F点,则△AED的面积:四边形ADGF的面积=( )
A、BC=BE B、∠A=∠D C、∠ACB=∠DEB D、AC=DE7. 如图,G是△ABC的重心,直线L过A点与BC平行.若直线CG分别与AB,L交于D,E两点,直线BG与AC交于F点,则△AED的面积:四边形ADGF的面积=( )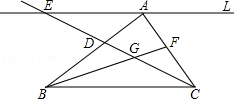 A、1:2 B、2:1 C、2:3 D、3:28. 如图,在△ABC中,D为BC的中点,过D点的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥GF,并交AB于点E,连接EG,EF.
A、1:2 B、2:1 C、2:3 D、3:28. 如图,在△ABC中,D为BC的中点,过D点的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥GF,并交AB于点E,连接EG,EF.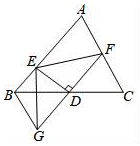 (1)、求证:BG=CF.(2)、请你猜想BE+CF与EF的大小关系,并说明理由.9. 如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:
(1)、求证:BG=CF.(2)、请你猜想BE+CF与EF的大小关系,并说明理由.9. 如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证: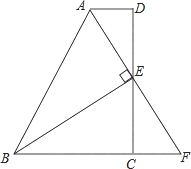 (1)、FC=AD;(2)、AB=BC+AD.10. 如图,点C在线段AB上,△ACD,△BCE都是等边三角形,AE交CD于点M,CE交BD于点N.
(1)、FC=AD;(2)、AB=BC+AD.10. 如图,点C在线段AB上,△ACD,△BCE都是等边三角形,AE交CD于点M,CE交BD于点N.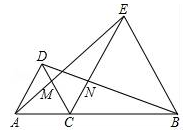 (1)、求证:△ ▲ ≌△ ▲ ;(先填写你认为正确的结论,再证明)(2)、求证:∠CME=∠BNC.11. △ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E , 连接PQ交AB于D.
(1)、求证:△ ▲ ≌△ ▲ ;(先填写你认为正确的结论,再证明)(2)、求证:∠CME=∠BNC.11. △ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E , 连接PQ交AB于D. (1)、当∠BQD=30°时,求AP的长;(2)、证明:在运动过程中,点D是线段PQ的中点;(3)、当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
(1)、当∠BQD=30°时,求AP的长;(2)、证明:在运动过程中,点D是线段PQ的中点;(3)、当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.三、中考演练