备考2020年高考数学一轮复习:03 逻辑联结词、全称量词与存在量词
试卷更新日期:2019-08-30 类型:一轮复习
一、单选题
-
1. 下列选项错误的是( )A、“ ”是“ ”的充分不必要条件. B、命题 “若 ,则 ”的逆否命题是“若 ,则 ” C、若命题“ ”,则“ ”. D、若“ ”为真命题,则 均为真命题.2. 命题 若 ,则 , 是 的逆命题,则( )A、 真, 真 B、 真, 假 C、 假, 真 D、 假, 假3. 命题 : , ;命题 : , .若 为假命题, 为真命题,则实数 的取值范围是( )A、 B、 C、 或 D、 或4. 下列说法正确的是( )A、命题“ ,使 ”的否定为“ ,都有 ” B、命题“若向量 与 的夹角为锐角,则 ”及它的逆命题均为真命题 C、命题“在锐角 中, ”为真命题 D、命题“若 ,则 或 ”的逆否命题为“若 且 ,则 ”5. 已知命题 : , ,则 为( )A、 , B、 , C、 , D、 ,6. 已知命题 , ; , ,若“ 且 ”为真命题,则实数 的取值范围是( )A、 B、 C、 D、7. 下列命题中为真命题的是( )A、命题“若
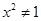 ,则
,则 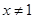 ”的逆命题
B、命题“若
”的逆命题
B、命题“若 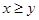 ,则
,则 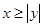 ”的否命题
C、命题“若 ,则
”的否命题
C、命题“若 ,则 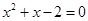 ”的逆命题
D、命题“若
”的逆命题
D、命题“若 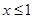 ,则
,则  ”的逆否命题
8. 若命题:“ , ”为假命题,则 的取值范围是( )A、 B、 C、 D、9. 已知p:2+2=5,q:3>2,则下列判断中,错误的是( )A、 或 为真,非 为假 B、 或 为真,非 为真 C、 且 为假,非 为假 D、 且 为假, 或 为真10. 已知命题 ,使 ;命题 ,则下列判断正确的是( )A、
”的逆否命题
8. 若命题:“ , ”为假命题,则 的取值范围是( )A、 B、 C、 D、9. 已知p:2+2=5,q:3>2,则下列判断中,错误的是( )A、 或 为真,非 为假 B、 或 为真,非 为真 C、 且 为假,非 为假 D、 且 为假, 或 为真10. 已知命题 ,使 ;命题 ,则下列判断正确的是( )A、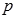 为真
B、
为真
B、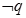 为假
C、
为假
C、 为真
D、
为真
D、 为假
11. 命题 : 中,若 ,则 ;命题 :若 ,则方程 一定无实根,则下列命题为真命题的是( )A、
为假
11. 命题 : 中,若 ,则 ;命题 :若 ,则方程 一定无实根,则下列命题为真命题的是( )A、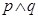 B、
B、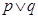 C、
C、 D、
D、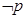 12. 命题 :若 ,则 ;命题 : ,使得 ,则下列命题中为真命题的是( )A、 B、 C、 D、
12. 命题 :若 ,则 ;命题 : ,使得 ,则下列命题中为真命题的是( )A、 B、 C、 D、二、填空题
-
13. 已知l,m是平面α外的两条不同直线.给出下列三个论断:
①l⊥m:②m∥α:③l⊥α.
以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:。
14. 若命题“ ,使得 成立”是假命题,则实数 的取值范围是 .15. 已知命题 , 是假命题,则实数 的取值范围是 .16. 命题“若整数a,b都是偶数,则 是偶数”的否命题可表示为 , 这个否命题是一个命题 可填:“真”,“假”之一17. 若“ , ”是真命题,则实数 的最小值为.三、解答题
-
18. 已知命题 : , ,命题 :点 在圆 的内部.(1)、若命题 为真命题,求实数 的取值范围;(2)、若命题“ 或 ”为假命题,求实数 的取值范围.19. 已知 ,
(Ⅰ)写出命题 的否定 ;命题 的否定 ;
(Ⅱ)若 为真命题,求实数 的取值范围.