2017年浙江省湖州市中考数学试卷
试卷更新日期:2017-06-27 类型:中考真卷
一、选择题:本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 实数 , , , 中,无理数是( )A、 B、 C、 D、2. 在平面直角坐标系中,点 关于原点的对称点 的坐标是( )A、 B、 C、 D、3.
如图,已知在 中, , , ,则 的值是( )
 A、 B、 C、 D、4. 一元一次不等式组 的解集是( )A、 B、 C、 D、 或5. 数据 , , , , , 的中位数是( )A、 B、 C、 D、6.
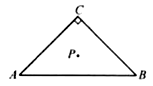
A、 B、 C、 D、4. 一元一次不等式组 的解集是( )A、 B、 C、 D、 或5. 数据 , , , , , 的中位数是( )A、 B、 C、 D、6.如图,已知在 中, , , ,点 是 的重心,则点 到 所在直线的距离等于( )
 A、 B、 C、 D、7. 一个布袋里装有 个只有颜色不同的球,其中 个红球, 个白球.从布袋里摸出 个球,记下颜色后放回,搅匀,再摸出 个球,则两次摸到的球都是红球的概率是( )A、 B、 C、 D、8.
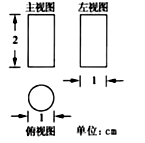
A、 B、 C、 D、7. 一个布袋里装有 个只有颜色不同的球,其中 个红球, 个白球.从布袋里摸出 个球,记下颜色后放回,搅匀,再摸出 个球,则两次摸到的球都是红球的概率是( )A、 B、 C、 D、8.如图是按 的比例画出的一个几何体的三视图,则该几何体的侧面积是( )
 A、 B、 C、 D、9.
A、 B、 C、 D、9.七巧板是我国祖先的一项卓越创造.下列四幅图中有三幅是小明用如图所示的七巧板拼成的,则不是小明拼成的那幅图是( )
 A、
A、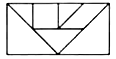 B、
B、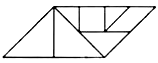 C、
C、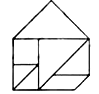 D、
D、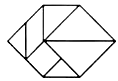 10.
10.在每个小正方形的边长为 的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距 的另一个格点的运动称为一次跳马变换.例如,在 的正方形网格图形中(如图1),从点 经过一次跳马变换可以到达点 , , , 等处.现有 的正方形网格图形(如图2),则从该正方形的顶点 经过跳马变换到达与其相对的顶点 ,最少需要跳马变换的次数是( )
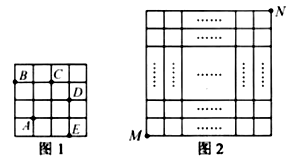 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分,满分24分,将答案填在答题纸上)
-
11. 把多项式 因式分解,正确的结果是 .12. 要使分式 有意义, 的取值应满足 .13. 已知一个多边形的每一个外角都等于 ,则这个多边形的边数是 .14.
如图,已知在 中, .以 为直径作半圆 ,交 于点 .若 ,则 的度数是度.
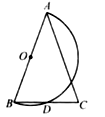 15.
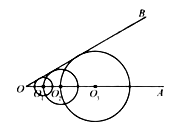
15.如图,已知 ,在射线 上取点 ,以 为圆心的圆与 相切;在射线 上取点 ,以 为圆心, 为半径的圆与 相切;在射线 上取点 ,以 为圆心, 为半径的圆与 相切; ;在射线 上取点 ,以 为圆心, 为半径的圆与 相切.若 的半径为 ,则 的半径长是 .
 16.
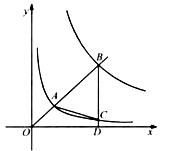
16.如图,在平面直角坐标系 中,已知直线 ( )分别交反比例函数 和 在第一象限的图象于点 , ,过点 作 轴于点 ,交 的图象于点 ,连结 .若 是等腰三角形,则 的值是 .
三、解答题 (本大题共8小题,共66分.解答应写出文字说明、证明过程或演算步骤.)
-
17. 计算: ..18. 解方程: .19. 对于任意实数 , ,定义关于“ ”的一种运算如下: .例如: ,(1)、若 ,求 的值;(2)、若 ,求 的取值范围.20.
为积极创建全国文明城市,某市对某路口的行人交通违章情况进行了 天的调查,将所得数据绘制成如下统计图(图2不完整):

请根据所给信息,解答下列问题:
(1)、第 天,这一路口的行人交通违章次数是多少次?这 天中,行人交通违章 次的有多少天?(2)、请把图2中的频数直方图补充完整;(3)、通过宣传教育后,行人的交通违章次数明显减少.经对这一路口的再次调查发现,平均每天的行人交通违章次数比第一次调查时减少了 次,求通过宣传教育后,这一路口平均每天还出现多少次行人的交通违章?21.如图, 为 的直角边 上一点,以 为半径的 与斜边 相切于点 ,交 于点 .已知 , .
 (1)、求 的长;(2)、求图中阴影部分的面积.22.
(1)、求 的长;(2)、求图中阴影部分的面积.22.已知正方形 的对角线 , 相交于点 .
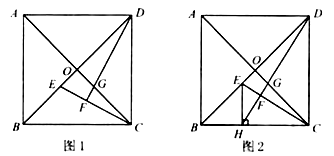 (1)、如图1, , 分别是 , 上的点, 与 的延长线相交于点 .若 ,求证: ;(2)、如图2, 是 上的点,过点 作 ,交线段 于点 ,连结 交 于点 ,交 于点 .若 ,
(1)、如图1, , 分别是 , 上的点, 与 的延长线相交于点 .若 ,求证: ;(2)、如图2, 是 上的点,过点 作 ,交线段 于点 ,连结 交 于点 ,交 于点 .若 ,①求证: ;
②当 时,求 的长.
23. 湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了 淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养 天的总成本为 万元;放养 天的总成本为 万元(总成本=放养总费用+收购成本).(1)、设每天的放养费用是 万元,收购成本为 万元,求 和 的值;(2)、设这批淡水鱼放养 天后的质量为 ( ),销售单价为 元/ .根据以往经验可知: 与 的函数关系为 ; 与 的函数关系如图所示.
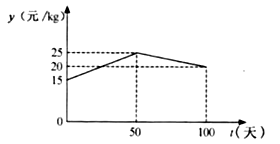
①分别求出当 和 时, 与 的函数关系式;
②设将这批淡水鱼放养 天后一次性出售所得利润为 元,求当 为何值时, 最大?并求出最大值.(利润=销售总额-总成本)
24.如图,在平面直角坐标系 中,已知 , 两点的坐标分别为 , , 是线段 上一点(与 , 点不重合),抛物线 ( )经过点 , ,顶点为 ,抛物线 ( )经过点 , ,顶点为 , , 的延长线相交于点 .
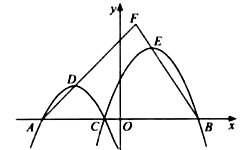 (1)、若 , ,求抛物线 , 的解析式;(2)、若 , ,求 的值;(3)、是否存在这样的实数 ( ),无论 取何值,直线 与 都不可能互相垂直?若存在,请直接写出 的两个不同的值;若不存在,请说明理由.
(1)、若 , ,求抛物线 , 的解析式;(2)、若 , ,求 的值;(3)、是否存在这样的实数 ( ),无论 取何值,直线 与 都不可能互相垂直?若存在,请直接写出 的两个不同的值;若不存在,请说明理由.