江苏省镇江市2019年中考数学试卷
试卷更新日期:2019-08-29 类型:中考真卷
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 一个物体如图所示,它的俯视图是( )
 A、
A、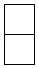 B、
B、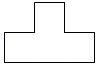 C、
C、 D、
D、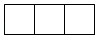 3. 如图,四边形 是半圆的内接四边形, 是直径, .若 ,则 的度数等于( )
3. 如图,四边形 是半圆的内接四边形, 是直径, .若 ,则 的度数等于( )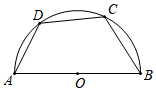 A、 B、 C、 D、4. 下列各数轴上表示的 的取值范围可以是不等式组 的解集的是( )A、
A、 B、 C、 D、4. 下列各数轴上表示的 的取值范围可以是不等式组 的解集的是( )A、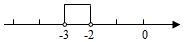 B、
B、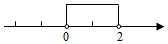 C、
C、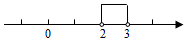 D、
D、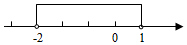 5. 如图,菱形 的顶点 、 在 轴上( 在 的左侧),顶点 、 在 轴上方,对角线 的长是 ,点 为 的中点,点 在菱形 的边上运动.当点 到 所在直线的距离取得最大值时,点 恰好落在 的中点处,则菱形 的边长等于( )
5. 如图,菱形 的顶点 、 在 轴上( 在 的左侧),顶点 、 在 轴上方,对角线 的长是 ,点 为 的中点,点 在菱形 的边上运动.当点 到 所在直线的距离取得最大值时,点 恰好落在 的中点处,则菱形 的边长等于( )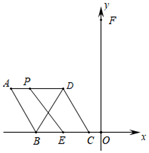 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
6. ﹣2019的相反数是 .7. 27的立方根为 .8. 一组数据 , , , , 的众数是 ,则 =.9. 若代数式 有意义,则实数 的取值范围是.10. 氢原子的半径约为 m,用科学记数法把 表示为.11. 已知点 、 都在反比例函数 的图象上,则 .(填“>”或“<”)12. 计算: =
13. 如图,直线 , 的顶点 在直线 上,边 与直线 相交于点 .若 是等边三角形, ,则 =°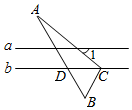 14. 已知关于 的方程 有两个相等的实数根,则 的值是..15. 将边长为 的正方形 绕点 按顺时针方向旋转到 的位置(如图),使得点 落在对角线 上, 与 相交于点 ,则 =.(结果保留根号)
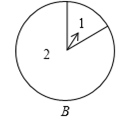
14. 已知关于 的方程 有两个相等的实数根,则 的值是..15. 将边长为 的正方形 绕点 按顺时针方向旋转到 的位置(如图),使得点 落在对角线 上, 与 相交于点 ,则 =.(结果保留根号)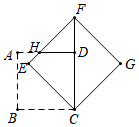 16. 如图,有两个转盘 、 ,在每个转盘各自的两个扇形区域中分别标有数字 、 ,分别转动转盘 、 ,当转盘停止转动时,若事件“指针都落在标有数字 的扇形区域内”的概率是 ,则转盘 中标有数字 的扇形的圆心角的度数是°.
16. 如图,有两个转盘 、 ,在每个转盘各自的两个扇形区域中分别标有数字 、 ,分别转动转盘 、 ,当转盘停止转动时,若事件“指针都落在标有数字 的扇形区域内”的概率是 ,则转盘 中标有数字 的扇形的圆心角的度数是°.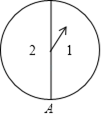
 17. 已知抛物线 过点 , 两点,若线段 的长不大于 ,则代数式 的最小值是.
17. 已知抛物线 过点 , 两点,若线段 的长不大于 ,则代数式 的最小值是.三、解答题
-
18.(1)、计算:(2)、化简: .19.(1)、解方程: ;(2)、解不等式: .20. 如图,四边形 中, ,点 、 分别在 上, ,过点 、 分别作 的垂线,垂足为 、 .
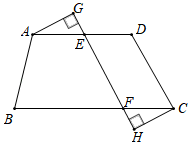 (1)、求证: ;(2)、连接 ,线段 与 是否互相平分?请说明理由.21. 小丽和小明将在下周的星期一到星期三这三天中各自任选一天担任值日工作,请用画树状图或列表格的方法,求小丽和小明在同一天值日的概率.22. 如图,在 中, ,过 延长线上的点 作 ,交 的延长线于点 ,以 为圆心, 长为半径的圆过点
(1)、求证: ;(2)、连接 ,线段 与 是否互相平分?请说明理由.21. 小丽和小明将在下周的星期一到星期三这三天中各自任选一天担任值日工作,请用画树状图或列表格的方法,求小丽和小明在同一天值日的概率.22. 如图,在 中, ,过 延长线上的点 作 ,交 的延长线于点 ,以 为圆心, 长为半径的圆过点 (1)、求证:直线 与 相切;(2)、若 , 的半径为 ,则 = .23. 如图,点 和点 是反比例函数 图象上的两点,一次函数 的图象经过点 ,与 轴交于点 ,与 轴交于点 ,过点 作 轴,垂足为 ,连接 .已知 与 的面积满足 .
(1)、求证:直线 与 相切;(2)、若 , 的半径为 ,则 = .23. 如图,点 和点 是反比例函数 图象上的两点,一次函数 的图象经过点 ,与 轴交于点 ,与 轴交于点 ,过点 作 轴,垂足为 ,连接 .已知 与 的面积满足 . (1)、 = , = ;(2)、已知点 在线段 上,当 时,求点 的坐标.24. 在三角形纸片 (如图1)中, , .小霞用 张这样的三角形纸片拼成了一个内外都是正五边形的图形(如图2).
(1)、 = , = ;(2)、已知点 在线段 上,当 时,求点 的坐标.24. 在三角形纸片 (如图1)中, , .小霞用 张这样的三角形纸片拼成了一个内外都是正五边形的图形(如图2).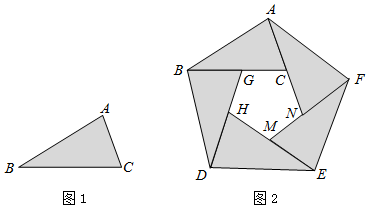 (1)、 °;(2)、求正五边形 的边 的长.参考值: , , .25. 陈老师对他所教的九(1)、九(2)两个班级的学生进行了一次检测,批阅后对最后一道试题的得分情况进行了归类统计(各类别的得分如下表),并绘制了如图所示的每班各类别得分人数的条形统计图(不完整).
(1)、 °;(2)、求正五边形 的边 的长.参考值: , , .25. 陈老师对他所教的九(1)、九(2)两个班级的学生进行了一次检测,批阅后对最后一道试题的得分情况进行了归类统计(各类别的得分如下表),并绘制了如图所示的每班各类别得分人数的条形统计图(不完整).各类别的得分表
得分
类别
:没有作答
:解答但没有正确
:只得到一个正确答案
:得到两个正确答案,解答完全正确
已知两个班一共有 的学生得到两个正确答案,解答完全正确,九(1)班学生这道试题的平均得分为 分.请解决如下问题:
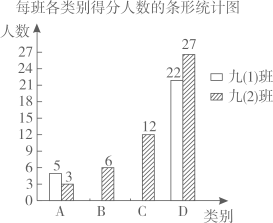 (1)、九(2)班学生得分的中位数是 ;(2)、九(1)班学生中这道试题作答情况属于 类和 类的人数各是多少?26. 【材料阅读】
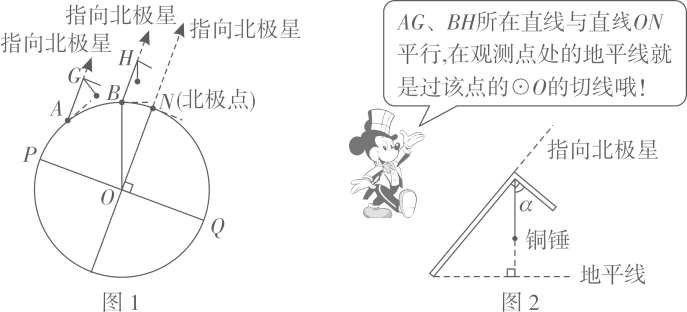
(1)、九(2)班学生得分的中位数是 ;(2)、九(1)班学生中这道试题作答情况属于 类和 类的人数各是多少?26. 【材料阅读】地球是一个球体,任意两条相对的子午线都组成一个经线圈(如图 中的 ).人们在北半球可观测到北极星,我国古人在观测北极星的过程中发明了如图 所示的工具尺(古人称它为“复矩”),尺的两边互相垂直,角顶系有一段棉线,棉线末端系一个铜锤,这样棉线就与地平线垂直.站在不同的观测点,当工具尺的长边指向北极星时,短边与棉线的夹角 的大小是变化的.
【实际应用】观测点 在图1所示的 上,现在利用这个工具尺在点 处测得 为 ,在点 所在子午线往北的另一个观测点 ,用同样的工具尺测得 为 . 是 的直径, .
 (1)、求 的度数;(2)、已知 km,求这两个观测点之间的距离即 上 的长.( 取 )27. 如图,二次函数 图象的顶点为 ,对称轴是直线 ,一次函数 的图象与 轴交于点 ,且与直线 关于 的对称直线交于点 .
(1)、求 的度数;(2)、已知 km,求这两个观测点之间的距离即 上 的长.( 取 )27. 如图,二次函数 图象的顶点为 ,对称轴是直线 ,一次函数 的图象与 轴交于点 ,且与直线 关于 的对称直线交于点 .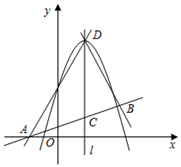 (1)、点 的坐标是;(2)、直线 与直线 交于点 , 是线段 上一点(不与点 、 重合),点 的纵坐标为 .过点 作直线与线段 、 分别交于点 , ,使得 与 相似.
(1)、点 的坐标是;(2)、直线 与直线 交于点 , 是线段 上一点(不与点 、 重合),点 的纵坐标为 .过点 作直线与线段 、 分别交于点 , ,使得 与 相似.①当 时,求 的长;
②若对于每一个确定的 的值,有且只有一个 与 相似,请直接写出 的取值范围.
28. 学校数学兴趣小组利用机器人开展数学活动.在相距 个单位长度的直线跑道 上,机器人甲从端点 出发,匀速往返于端点 、 之间,机器人乙同时从端点 出发,以大于甲的速度匀速往返于端点 、 之间.他们到达端点后立即转身折返,用时忽略不计.兴趣小组成员探究这两个机器人迎面相遇的情况,这里的“迎面相遇”包括面对面相遇、在端点处相遇这两种.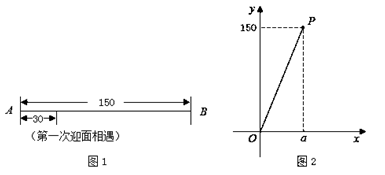 (1)、【观察】
(1)、【观察】①观察图 ,若这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,则他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度;
②若这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,则他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度;
(2)、【发现】设这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度.兴趣小组成员发现了 与 的函数关系,并画出了部分函数图象(线段 ,不包括点 ,如图 所示).
① =;
②分别求出各部分图象对应的函数表达式,并在图 中补全函数图象;
(3)、【拓展】设这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,他们第三次迎面相遇时,相遇地点与点 之间的距离为 个单位长度.若这两个机器人第三次迎面相遇时,相遇地点与点 之间的距离 不超过 个单位长度,则他们第一次迎面相遇时,相遇地点与点 之间的距离 的取值范围是.(直接写出结果)