广西百色市2019年中考数学试卷
试卷更新日期:2019-08-29 类型:中考真卷
一、单选题
-
1. 三角形的内角和等于( )A、 B、 C、 D、2. 如图,已知 ,则 的大小是( )
 A、 B、 C、 D、3. 一组数据2,6,4,10,8,12的中位数是( )A、6 B、7 C、8 D、94. 方程 的解是( )A、无解 B、 C、 D、5. 下列几何体中,俯视图不是圆的是( )A、
A、 B、 C、 D、3. 一组数据2,6,4,10,8,12的中位数是( )A、6 B、7 C、8 D、94. 方程 的解是( )A、无解 B、 C、 D、5. 下列几何体中,俯视图不是圆的是( )A、 四面体
B、
四面体
B、 圆锥
C、
圆锥
C、 球
D、
球
D、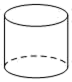 圆柱
6. 一周时间有604800秒,604800用科学记数法表示为( )A、 B、 C、 D、7. 下列图形,既是轴对称图形又是中心对称图形的是( )A、正三角形 B、正五边形 C、等腰直角三角形 D、矩形8. 不等式组 的解集是( )A、 B、 或 C、 D、9. 抛物线 可由抛物线 如何平移得到的( )A、先向左平移3个单位,再向下平移2个单位 B、先向左平移6个单位,再向上平移7个单位 C、先向上平移2个单位,再向左平移3个单位 D、先回右平移3个单位,再向上平移2个单位10. 小韦和小黄进行射击比赛,各射击6次,根据成绩绘制的两幅折线统计图如下,以下判断正确的是( )
圆柱
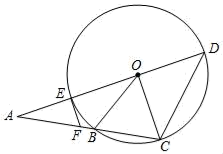
6. 一周时间有604800秒,604800用科学记数法表示为( )A、 B、 C、 D、7. 下列图形,既是轴对称图形又是中心对称图形的是( )A、正三角形 B、正五边形 C、等腰直角三角形 D、矩形8. 不等式组 的解集是( )A、 B、 或 C、 D、9. 抛物线 可由抛物线 如何平移得到的( )A、先向左平移3个单位,再向下平移2个单位 B、先向左平移6个单位,再向上平移7个单位 C、先向上平移2个单位,再向左平移3个单位 D、先回右平移3个单位,再向上平移2个单位10. 小韦和小黄进行射击比赛,各射击6次,根据成绩绘制的两幅折线统计图如下,以下判断正确的是( )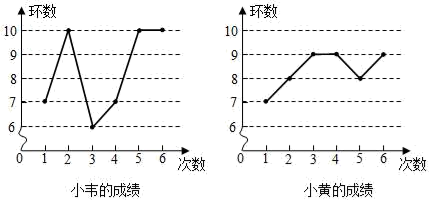 A、小黄的成绩比小韦的成绩更稳定 B、两人成绩的众数相同 C、小韦的成绩比小黄的成绩更稳定 D、两人的平均成绩不相同11. 下列四个命题:①两直线平行,内错角相等;②对顶角相等;③等腰三角形的两个底角相等;④菱形的对角线互相垂直,其中逆命题是真命题的是( )A、①②③④ B、①③④ C、①③ D、①12. 阅读理解:已知两点 ,则线段 的中点 的坐标公式为: , .如图,已知点 为坐标原点,点 , 经过点 ,点 为弦 的中点.若点 ,则有 满足等式: .设 ,则 满足的等式是( )
A、小黄的成绩比小韦的成绩更稳定 B、两人成绩的众数相同 C、小韦的成绩比小黄的成绩更稳定 D、两人的平均成绩不相同11. 下列四个命题:①两直线平行,内错角相等;②对顶角相等;③等腰三角形的两个底角相等;④菱形的对角线互相垂直,其中逆命题是真命题的是( )A、①②③④ B、①③④ C、①③ D、①12. 阅读理解:已知两点 ,则线段 的中点 的坐标公式为: , .如图,已知点 为坐标原点,点 , 经过点 ,点 为弦 的中点.若点 ,则有 满足等式: .设 ,则 满足的等式是( )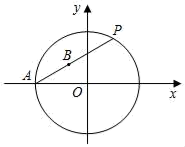 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 的相反数是.14. 若式子 在实数范围内有意义,则 的取值范围是.15. 编号为2,3,4,5,6的乒乓球放在不透明的袋内,从中任抽一个球,抽中编号是偶数的概率是.16. 观察一列数: ,0,3,6,9,12,…,按此规律,这一列数的第21个数是.17. 如图, 与 是以坐标原点 为位似中心的位似图形,若点 , , 则 的面积为.
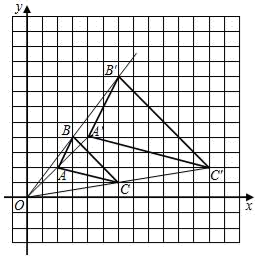 18. 四边形具有不稳定性.如图,矩形 按箭头方向变形成平行四边形 ,当变形后图形面积是原图形面积的一半时,则 .
18. 四边形具有不稳定性.如图,矩形 按箭头方向变形成平行四边形 ,当变形后图形面积是原图形面积的一半时,则 .
三、解答题
-
19. 计算:20. 求式子 的值,其中 .21. 如图,已知平行四边形 中,点 为坐标顶点,点 ,函数 的图象经过点 .
 (1)、求 的值及直线 的函数表达式:(2)、求四边形 的周长.22. 如图,菱形 中,作 、 ,分别交 、 的延长线于点 .
(1)、求 的值及直线 的函数表达式:(2)、求四边形 的周长.22. 如图,菱形 中,作 、 ,分别交 、 的延长线于点 .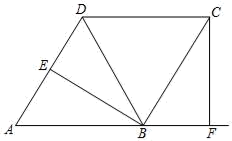 (1)、求证: ;(2)、若点 恰好是 的中点, ,求 的值.23. 九年级(1)班全班50名同学组成五个不同的兴趣爱好小组,每人都参加且只能参加一个小组,统计(不完全)人数如下表:
(1)、求证: ;(2)、若点 恰好是 的中点, ,求 的值.23. 九年级(1)班全班50名同学组成五个不同的兴趣爱好小组,每人都参加且只能参加一个小组,统计(不完全)人数如下表:编号
一
二
三
四
五
人数
15
20
10
已知前面两个小组的人数之比是 .
解答下列问题:
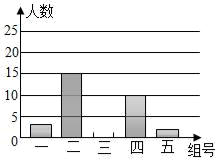 (1)、 .(2)、补全条形统计图:(3)、若从第一组和第五组中任选两名同学,求这两名同学是同一组的概率.(用树状图或列表把所有可能都列出来)24. 一艘轮船在相距90千米的甲、乙两地之间匀速航行,从甲地到乙地顺流航行用6小时,逆流航行比顺流航行多用4小时.(1)、求该轮船在静水中的速度和水流速度;(2)、若在甲、乙两地之间建立丙码头,使该轮船从甲地到丙地和从乙地到丙地所用的航行时间相同,问甲、丙两地相距多少千米?
(1)、 .(2)、补全条形统计图:(3)、若从第一组和第五组中任选两名同学,求这两名同学是同一组的概率.(用树状图或列表把所有可能都列出来)24. 一艘轮船在相距90千米的甲、乙两地之间匀速航行,从甲地到乙地顺流航行用6小时,逆流航行比顺流航行多用4小时.(1)、求该轮船在静水中的速度和水流速度;(2)、若在甲、乙两地之间建立丙码头,使该轮船从甲地到丙地和从乙地到丙地所用的航行时间相同,问甲、丙两地相距多少千米?