2016-2017学年湖北省襄阳市老河口市七年级下学期期中数学试卷
试卷更新日期:2017-06-27 类型:期中考试
一、选择题
-
1. 下列图形中,∠1与∠2是对顶角的是( )A、
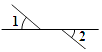 B、
B、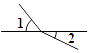 C、
C、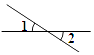 D、
D、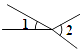 2. 下列图形中线段PQ的长度表示点P到直线a的距离的是( )A、
2. 下列图形中线段PQ的长度表示点P到直线a的距离的是( )A、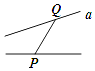 B、
B、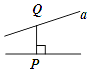 C、
C、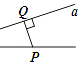 D、
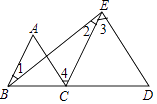
D、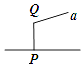 3. 4的平方根是( )A、2 B、﹣2 C、± D、±24. 如图,下列条件中不能判定AD∥BC的是( )
3. 4的平方根是( )A、2 B、﹣2 C、± D、±24. 如图,下列条件中不能判定AD∥BC的是( ) A、∠BAD+∠ABC=180° B、∠1=∠2 C、∠3=∠4 D、∠BAD=∠BCD5. 下列点中,位于直角坐标系第二象限的点是( )A、(2,1) B、(﹣2,﹣1) C、(﹣2,1) D、(2,﹣1)6. 若点P(x,y)的坐标满足xy=0,则点P的位置是( )A、在x轴上 B、在y轴上 C、是坐标原点 D、在x轴上或在y轴上7. 下列各数的立方根是﹣2的数是( )A、4 B、﹣4 C、8 D、﹣88. 点C在x轴上方,y轴左侧,距离x轴2个单位长度,距离y轴3个单位长度,则点C的坐标为( )A、(﹣3,2) B、(﹣2,﹣3) C、(﹣2,3) D、( 3,﹣2)9. 下列四个实数中,是无理数的为( )A、 B、 C、0 D、0.10. 下列语句中正确的是( )A、正整数和负整数统称为整数 B、有理数和无理数统称为实数 C、开方开不尽的数和π统称为无理数 D、正数、0、负数统称为有理数11. 线段AB两端点坐标分别为A(﹣1,4),B(4,﹣2),现将线段AB平移后点A的对应点坐标为(﹣4,2),则点B的对应点的坐标为( )A、(1,4) B、(1,﹣4) C、(2,﹣5) D、(1,0)12. 下列各语句:①对顶角相等吗?②延长线段AB;③内错角相等;④垂线段最短.其中真命题有( )A、1个 B、2个 C、3个 D、4个
A、∠BAD+∠ABC=180° B、∠1=∠2 C、∠3=∠4 D、∠BAD=∠BCD5. 下列点中,位于直角坐标系第二象限的点是( )A、(2,1) B、(﹣2,﹣1) C、(﹣2,1) D、(2,﹣1)6. 若点P(x,y)的坐标满足xy=0,则点P的位置是( )A、在x轴上 B、在y轴上 C、是坐标原点 D、在x轴上或在y轴上7. 下列各数的立方根是﹣2的数是( )A、4 B、﹣4 C、8 D、﹣88. 点C在x轴上方,y轴左侧,距离x轴2个单位长度,距离y轴3个单位长度,则点C的坐标为( )A、(﹣3,2) B、(﹣2,﹣3) C、(﹣2,3) D、( 3,﹣2)9. 下列四个实数中,是无理数的为( )A、 B、 C、0 D、0.10. 下列语句中正确的是( )A、正整数和负整数统称为整数 B、有理数和无理数统称为实数 C、开方开不尽的数和π统称为无理数 D、正数、0、负数统称为有理数11. 线段AB两端点坐标分别为A(﹣1,4),B(4,﹣2),现将线段AB平移后点A的对应点坐标为(﹣4,2),则点B的对应点的坐标为( )A、(1,4) B、(1,﹣4) C、(2,﹣5) D、(1,0)12. 下列各语句:①对顶角相等吗?②延长线段AB;③内错角相等;④垂线段最短.其中真命题有( )A、1个 B、2个 C、3个 D、4个二、填空题
-
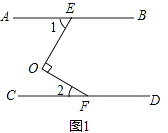
13. 如图,直线AB,CD相交于点O,若∠AOC+∠BOD=100°,则∠AOD等于
度.
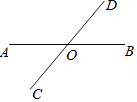 14. 如果某一个数的一个平方根是﹣3,那么这个数是 .15. 如果a与b互为倒数,c与d互为相反数,那么﹣ ﹣1的值是 .16. 若点M(m﹣3,m+1)在平面直角坐标系的y轴上,则点M的坐标为 .17. 如图,OA⊥OB,∠AOC=120°,则∠BOC等于度.
14. 如果某一个数的一个平方根是﹣3,那么这个数是 .15. 如果a与b互为倒数,c与d互为相反数,那么﹣ ﹣1的值是 .16. 若点M(m﹣3,m+1)在平面直角坐标系的y轴上,则点M的坐标为 .17. 如图,OA⊥OB,∠AOC=120°,则∠BOC等于度.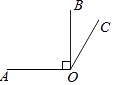 18. 在平面直角坐标系中,若点M(1,3)与点N(x,3)之间的距离是5,则x的值是 .19. 已知正方形ABCD的三个顶点A(﹣4,0),B(0,0),C(0,4),则第四个顶点D的坐标为 .20. 命题“同旁内角的平分线互相垂直”是命题(填“真”或“假”).21. 若x,y都是实数,且 ,则x+3y的立方根为 .22. 如图,a∥b,∠2=∠3,∠1=40°,则∠4的度数是度.
18. 在平面直角坐标系中,若点M(1,3)与点N(x,3)之间的距离是5,则x的值是 .19. 已知正方形ABCD的三个顶点A(﹣4,0),B(0,0),C(0,4),则第四个顶点D的坐标为 .20. 命题“同旁内角的平分线互相垂直”是命题(填“真”或“假”).21. 若x,y都是实数,且 ,则x+3y的立方根为 .22. 如图,a∥b,∠2=∠3,∠1=40°,则∠4的度数是度.
三、解答题:
-
23. 计算:(1)、 ×(2)、 + .24. 已知x的两个不同的平方根分别是a+3和2a﹣15,且 =4,求x,y的值.25. 如图所示,直线AB、CD、EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=70°,求∠DOG的度数.
 26. 已知点P(2m+4,m﹣1),请分别根据下列条件,求出点P的坐标.(1)、点P的纵坐标比横坐标大3;(2)、点P在过A(2,﹣4)点,且与y轴平行的直线上;(3)、点P到两坐标轴的距离相等.27. 如图,已知火车站的坐标为(2,2),文化宫的坐标为(﹣1,3).
26. 已知点P(2m+4,m﹣1),请分别根据下列条件,求出点P的坐标.(1)、点P的纵坐标比横坐标大3;(2)、点P在过A(2,﹣4)点,且与y轴平行的直线上;(3)、点P到两坐标轴的距离相等.27. 如图,已知火车站的坐标为(2,2),文化宫的坐标为(﹣1,3). (1)、请你根据题目条件,画出平面直角坐标系;(2)、写出体育场,市场,超市的坐标;(3)、已知游乐场A,图书馆B,公园C的坐标分别为(0,5),(﹣2,﹣2),(2,﹣2),请在图中标出A,B,C的位置.
(1)、请你根据题目条件,画出平面直角坐标系;(2)、写出体育场,市场,超市的坐标;(3)、已知游乐场A,图书馆B,公园C的坐标分别为(0,5),(﹣2,﹣2),(2,﹣2),请在图中标出A,B,C的位置.