2017年广东省深圳市中考数学试卷
试卷更新日期:2017-06-27 类型:中考真卷
一、选择题
-
1. -2的绝对值是( )A、-2 B、2 C、 D、2.
图中立体图形的主视图是( )
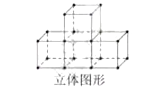 A、
A、 B、
B、 C、
C、 D、
D、 3. 随着“一带一路”建设的不断发展,我国已与多个国家建立了经贸合作关系,去年中哈铁路(中国至哈萨克斯坦)运输量达8200000吨,将8200000用科学记数法表示为( )A、 B、 C、 D、4. 观察下列图形,其中既是轴对称又是中心对称图形的是( )A、
3. 随着“一带一路”建设的不断发展,我国已与多个国家建立了经贸合作关系,去年中哈铁路(中国至哈萨克斯坦)运输量达8200000吨,将8200000用科学记数法表示为( )A、 B、 C、 D、4. 观察下列图形,其中既是轴对称又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5.
5.下列选项中,哪个不可以得到 ?( )
 A、 B、 C、 D、6. 不等式组 的解集为( )A、 B、 C、或 D、7. 一球鞋厂,现打折促销卖出330双球鞋,比上个月多卖10%,设上个月卖出 双,列出方程( )A、 B、 C、 D、8.
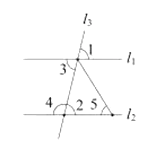
A、 B、 C、 D、6. 不等式组 的解集为( )A、 B、 C、或 D、7. 一球鞋厂,现打折促销卖出330双球鞋,比上个月多卖10%,设上个月卖出 双,列出方程( )A、 B、 C、 D、8.如图,已知线段 ,分别以 为圆心,大于 为半径作弧,连接弧的交点得到直线 ,在直线 上取一点 ,使得 ,延长 至 ,求 的度数为( )
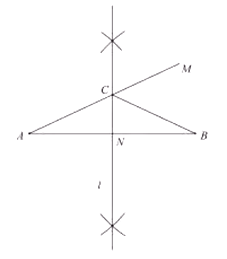 A、 B、 C、 D、9. 下列哪一个是假命题( )A、五边形外角和为 B、切线垂直于经过切点的半径 C、关于 轴的对称点为 D、抛物线 对称轴为直线10. 某共享单车前 公里1元,超过 公里的,每公里2元,若要使使用该共享单车50%的人只花1元钱, 应该要取什么数( )A、平均数 B、中位数 C、众数 D、方差11.
A、 B、 C、 D、9. 下列哪一个是假命题( )A、五边形外角和为 B、切线垂直于经过切点的半径 C、关于 轴的对称点为 D、抛物线 对称轴为直线10. 某共享单车前 公里1元,超过 公里的,每公里2元,若要使使用该共享单车50%的人只花1元钱, 应该要取什么数( )A、平均数 B、中位数 C、众数 D、方差11.如图,学校环保社成员想测量斜坡 旁一棵树 的高度,他们先在点 处测得树顶 的仰角为 ,然后在坡顶 测得树顶 的仰角为 ,已知斜坡 的长度为 , 的长为 ,则树 的高度是( )
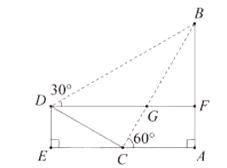 A、 B、30 C、 D、4012.
A、 B、30 C、 D、4012.如图,正方形 的边长是3, ,连接 交于点 ,并分别与边 交于点 ,连接 .下列结论:① ;② ;③ ;④当 时, .其中正确结论的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 因式分解: .14. 在一个不透明的袋子里,有2个黑球和1个白球,除了颜色外全部相同,任意摸两个球,摸到1黑1白的概率是 .15. 阅读理解:引入新数 ,新数 满足分配律,结合律,交换律,已知 ,那么 .16.
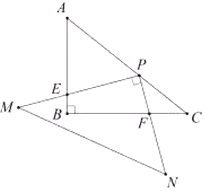
如图,在 中, , , , , ,点 在 上, 交 于点 , 交 于点 ,当 时, .
三、解答题
-
17. 计算 .18. 先化简,再求值: ,其中 .19.
深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.
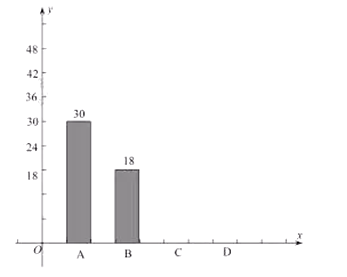
类型
频数
频率
A
30
B
18
0.15
C
0.40
D
(1)、学生共人, , ;(2)、补全条形统计图;(3)、若该校共有2000人,骑共享单车的有人.20. 一个矩形周长为56厘米.(1)、当矩形面积为180平方厘米时,长宽分别为多少?(2)、能围成面积为200平方厘米的矩形吗?请说明理由.21. 如图一次函数 与反比例函数 交于 、 ,与 轴, 轴分别交于点 .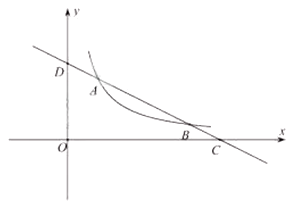 (1)、直接写出一次函数 的表达式和反比例函数 的表达式;(2)、求证: .
(1)、直接写出一次函数 的表达式和反比例函数 的表达式;(2)、求证: .