高数统编版第一册 2.2 基本不等式同步训练

试卷更新日期：2019-08-28 类型：同步测试

进入出卷网下载

1. 三国时期赵爽在《勾股方圆图注》中对勾股定理的证明可用现代数学表述为如图所示，我们教材中利用该图作为“（）”的几何解释．

A、如果a＞b，b＞c，那么a＞c B、如果a＞b＞0，那么a²＞b² C、对任意实数a和b，有a²+b²≥2ab，当且仅当a=b时等号成立 D、如果a＞b，c＞0那么ac＞bc

查看试题解析
2. 若 $a > 0$ ， $b > 0$ 且 $2 a + b = 4$ ，则 $\frac{1}{a b}$ 的最小值为（）

A、2 B、 $\frac{1}{2}$ C、4 D、 $\frac{1}{4}$

查看试题解析
3. 已知 $a + b = 2$ ，则 $3^{a} + 3^{b}$ 的最小值是（）

A、 $2 \sqrt{3}$ B、 $6$ C、 $2$ D、 $2 \sqrt{2}$

查看试题解析
4. 用长度为24的材料围一矩形场地，中间加两道隔墙，要使矩形的面积最大，则隔墙的长度为（）

A、3 B、4 C、6 D、12

查看试题解析
5. 若 $x > 2$ ，则 $x + \frac{4}{x - 2}$ 的最小值为（）

A、2 B、4 C、6 D、8

查看试题解析
6. 若a>0，b>0，且a＋b＝4，则下列不等式恒成立的是（）

A、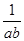 > $\frac{1}{2}$ B、＋ ≤1 C、 $\sqrt{a b}$ ≥2 D、a²＋b²≥8

查看试题解析

11. 已知x＞0，y＞0，且x＋4y－2xy＝0，
求：

(1)、xy的最小值；

(2)、x＋y的最小值．

查看试题解析
12. 已知 $a ， b ， c$ 是全不相等的正实数，证明： $\frac{b + c - a}{a} + \frac{a + c - b}{b} + \frac{a + b - c}{c} > 3$ .

查看试题解析
13.

(1)、已知 $x > 3$ ，求 $y = x + \frac{4}{x - 3}$ 的最小值，并求取到最小值时x的值；

(2)、已知 $x > 0$ ， $y > 0$ ， $\frac{x}{2} + \frac{y}{3} = 2$ ，求xy的最大值，并求取到最大值时x、y的值．

查看试题解析
14. 某村计划建造一个室内面积为800m²的矩形蔬菜温室，在室内，沿左、右两侧与后侧内墙各保留1m宽的通道，沿前侧内墙保留3m宽的空地.当矩形温室的边长各为多少时，蔬菜的种植面积最大？最大种植面积是多少？

查看试题解析